|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Об одной задаче самой 1-ой венгерской олимпиады (1894)
Внутри некоторой окружности даны точки P и Q . Построить вписанный в окружность прямоугольный треугольник, на одном из катетов которого лежит Р, а на другом - Q. При каких P и Q задача разрешима?
Задача собственно совсем простенькая:
Решение - Вершина искомого треугольника - точка(точки) пересечения окружности с диаметром PQ с исходной окружностью. Решения нет, если эта окружность не пересекается с исходной. Но некоторое чувство неудовлетворённости. Хотелось бы как-то охарактеризовать такое расположение точек Р и Q . А я не вижу как. |
|
|
| номер сообщения: 49-47-43788 |
|
|
|
|
Grigoriy: Об одной задаче самой 1-ой венгерской олимпиады (1894)
Внутри некоторой окружности даны точки P и Q . Построить вписанный в окружность прямоугольный треугольник, на одном из катетов которого лежит Р, а на другом - Q. При каких P и Q задача разрешима?
Задача собственно совсем простенькая:
Решение - Вершина искомого треугольника - точка(точки) пересечения окружности с диаметром PQ с исходной окружностью. Решения нет, если эта окружность не пересекается с исходной. Но некоторое чувство неудовлетворённости. Хотелось бы как-то охарактеризовать такое расположение точек Р и Q . А я не вижу как. |
Вроде бы решений нет, если "расстояние между центрами двух окружностей меньше разницы радиусов соответствующих окружностей". |
|
|
| номер сообщения: 49-47-43790 |
|
|
|
|
Григорий, наверное, имеет в виду, что если поместить точку Р в начало координат (центр круга), то при движении ее, например, по оси х, каждой точке будет взаимооднозначно соответствовать некая область в круге, подходящая "решению". И он хотел бы увидеть красоту алгебраической либо геометрической зависимости.
Например, если поместить точку Р в центр круга, то все "подходящие" точки Q будут находиться в кольце между r круга и r пополам.
А если наоборот, поставить Р на окружности, то ответом будет вообще любая точка круга. |
|
|
| номер сообщения: 49-47-43791 |
|
|
|
|
Решение я получил алгебраически, но оно геометрически красивое. Если взять единичную окружность, и точку P на оси ординат с координатами (0, p), то область решений для точки Q - это круг с вырезанным эллипсом:
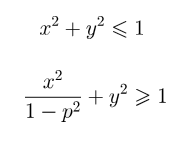
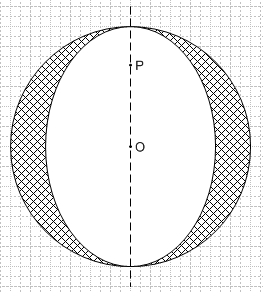 |
|
|
| номер сообщения: 49-47-43798 |
|
|
|
|
jenya: Умер Сергей Петрович Новиков.
| Филдсовская премия (1970), Премия Лобачевского (1981), Премия Вольфа (2005), премия Погорелова (2008), медаль Боголюбова (2009), медаль Эйлера (2012). |
|
Кстати, племянник Мистислава Келдыша и брат Леонида Келдыша.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43818 |
|
|
|
|
Список(по моему разумению) математиков высшего ранга
Фалес, Евдокс, Теэтет, Архимед, Диофант, Виет, Ферма, Декарт, Ньютон, Лейбниц, Эйлер, Лагранж, Абель, Галуа, Коши, Гаусс, Дирихле, Вейерштрасс, Риман, Ли, Кантор, Пуанкаре, Гильберт, Гёдель, Колмогоров, Гротендик.
Обсуждение приветствуется :-)
Если пройти по ссылке, там в списке нет Гёделя и Колмогорова. Решил добавить по обсуждениям там. |
|
|
| номер сообщения: 49-47-43831 |
|
|
|
|
Евклид
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43832 |
|
|
|
|
| номер сообщения: 49-47-43833 |
|
|
|
|
| Евклид конечно написал в блестящем стиле энциклопедию(видимо) всего к тому моменту известного, но его личный вклад мне кажется сравнительно небольшим. |
|
|
| номер сообщения: 49-47-43834 |
|
|
|
|
Это дело тёмное, а народу известно, что он геометрию придумал.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43835 |
|
|
|
|
А где Пифагор?
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43836 |
|
|
|
|
| номер сообщения: 49-47-43837 |
|
|
|
|
| номер сообщения: 49-47-43838 |
|
|
|
|
| По ссылке Пифагор обсуждается, в частности Нагир за него ратует, но на самом деле что именно он сделал как мне кажется совершенно неизвестно. |
|
|
| номер сообщения: 49-47-43839 |
|
|
|
|
Как мне кажется, несмотря на реальное их величие, они сделали существенно меньше людей из списка. Но моё мнение, конечно, понаслышечное. Впрочем, подозреваю, и Ваше :-) |
|
|
| номер сообщения: 49-47-43840 |
|
|
|
|
| Это точно: я - филолог. Ещё я слышал про Кеплера, Монжа и Выгодского)) |
|
|
| номер сообщения: 49-47-43841 |
|
|
|
|
Я бы, как физик, танцевал от Ньютона, Лейбница, Эйлера, Лагранжа и Гаусса.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43842 |
|
|
|
|
Математик изначально не может не быть философом, а физик с некоторых пор поставлен перед выбором - или ты с нами, или - вон с теми.  |
|
|
| номер сообщения: 49-47-43843 |
|
|
|
|
| Если бы я был физиком, то Гамильтона бы добавил. Но так-как я не физик, то принимаю список Григория. |
|
|
| номер сообщения: 49-47-43844 |
|
|
|
|
Гамильтона поддерживаю. Как минимум за комплексные числа и "канонические" уравнения теоретической механики. Ну и слово Hamiltonian...
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43845 |
|
|
|
|
Billy Bоnes: Математик изначально не может не быть философом.  |
Пифагор.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43846 |
|
|
|
|
| Quantrinas: Гамильтона поддерживаю. Как минимум за комплексные числа и "канонические" уравнения теоретической механики. Ну и слово Hamiltonian... |
Quantrinas: Billy Bоnes: Математик изначально не может не быть философом.  |
Пифагор. |
А Пифагора за штаны? 
Я слышал, диетолог он был никак не в меньшей степени, чем математик.  |
|
|
| номер сообщения: 49-47-43847 |
|
|
|
|
Пифагора за то, что ввёл математику в число важных знаний.
И пытался применять для объяснения природы.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43848 |
|
|
|
|
| Вот до чего довел попсовый хитпарад, затеянный Григорием. |
|
|
| номер сообщения: 49-47-43849 |
|
|
|
|
| Может быть ещё Блез Паскаль и Христиан Гюйгенс? |
|
|
| номер сообщения: 49-47-43850 |
|
|
|
|
| номер сообщения: 49-47-43851 |
|
|
|
|
Мёбиус это совсем не в кассу. Рядом с Паскалем жили Декарт и Ферма - явно крупнее, намного больше сделавшие.
Пифагор - мы же ничего не знаем о его вкладе в математику, а идея о гармонии мира, выражаемой числами имхо скорее поэтическая, чем математическая и даже философская.
Гюйгенс и Гамильтон конечно великие, может даже гении, но великих учёных и даже гениев много. Вот прямо сейчас живут безусловные(имхо) гении - Милнор, Смейл, Серр, Громов, Ленглендс, Дринфельд, Хиронака, Делинь, Дональдсон, Виттен, Фальтингс, Шольце, Тао.
Это о ком я имею представление(смутное, моя квалификация очень невелика), наверняка есть ещё.
В моём списке - те, кто мне представляются самыми-самыми. |
|
|
| номер сообщения: 49-47-43852 |
|
|
|
|
| Quantrinas: Гамильтона поддерживаю. Как минимум за комплексные числа и "канонические" уравнения теоретической механики. Ну и слово Hamiltonian... |
Какое отношение Гамильтон имеет к комплексным числам? |
|
|
| номер сообщения: 49-47-43853 |
|
|
|
|
Если верить Википедии, то
| В 1835 году Гамильтон опубликовал работу «Теория алгебраических пар» (Theory of Algebraic Couples), в которой дал строгое построение теории комплексных чисел. |
Ну и кватернионы конечно, хотя я на являюсь их прямым поклонником, но они явно аналогичны 4-мерному пространству-времени.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-47-43854 |
|
|
|
|
Quantrinas: Если верить Википедии, то
| В 1835 году Гамильтон опубликовал работу «Теория алгебраических пар» (Theory of Algebraic Couples), в которой дал строгое построение теории комплексных чисел. |
|
Очень сомнительно, чтобы в этой работе было что-то новое и значительное именно относительно комплексных чисел. |
|
|
| номер сообщения: 49-47-43855 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2025 гг. |
|
|
|