|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
zak06: Если какая-то разность а(к1)-а(к2) равна какой то другой разности
а(к3)-а(к4), то ясно, что могут быть два разных маршрута с одинаковой полной суммой. Это и дает минимальную цену наиболее дорогого билета. |
Откровенно говоря, я ничего не понял. |
|
|
| номер сообщения: 49-2-3687 |
|
|
|
|
| dimarko:В чем фокус-то, товарищи математики? |
Отличное наблюдение. Фокус в том, что пары 1 и 9, 2 и 8, 3 и 7, 4 и 6 будут парами противоположных точек на любом маршруте (включая маршруты коня). А сумма чисел в каждой паре - 10. А любое 8-значное число, у которого суммы 1 и 5 цифры, 2 и 6 цифры, 3 и 7 цифры и 4 и 8 цифры равны, делится на 1111. |
|
|
| номер сообщения: 49-2-3688 |
|
|
|
|
iourique: | dimarko:В чем фокус-то, товарищи математики? |
Отличное наблюдение. Фокус в том, что пары 1 и 9, 2 и 8, 3 и 7, 4 и 6 будут парами противоположных точек на любом маршруте (включая маршруты коня). А сумма чисел в каждой паре - 10. А любое 8-значное число, у которого суммы 1 и 5 цифры, 2 и 6 цифры, 3 и 7 цифры и 4 и 8 цифры равны, делится на 1111. |
Кстати, всего 384 таких 8-значных чисел из цифр (1,2,3,4,6,7,8,9), кратных 1111:
от 12349876=1111*11116 до 98761234=1111*88894.
__________________________
I love chess |
|
|
| номер сообщения: 49-2-3689 |
|
|
|
|
MikhailK: zak06: Если какая-то разность а(к1)-а(к2) равна какой то другой разности
а(к3)-а(к4), то ясно, что могут быть два разных маршрута с одинаковой полной суммой. Это и дает минимальную цену наиболее дорогого билета. |
Откровенно говоря, я ничего не понял. |
Все выяснилось, я решал СОВСЕМ ДРУГУЮ задачу(?!) Сорри...
__________________________
I love chess |
|
|
| номер сообщения: 49-2-3690 |
|
|
|
|
| MikhailK: Возможно мы решаем разные задачи, но у меня максимальная стоимость билета равна 221. |
Теперь и я получил 221 (2 разными способами), но доказывать как не умел, так и не умею :( |
|
|
| номер сообщения: 49-2-3691 |
|
|
|
|
Навеяло:
http://en.wikipedia.org/wiki/Golomb_ruler |
|
|
| номер сообщения: 49-2-3692 |
|
|
|
|
Sad_Donkey: iourique:
Ну, что вы... Какие счеты... |
А вот теперь, кажется, решил: C(k) > ln k/ln 4.
|
Думаю, что решили. Честно сказать, мне не хочется "досимвольно" разбираться в том, что вы написали. Но идея и "ключевое неравенство" похожи на то, что было у меня при решении этой задачи. И, надо полагать, соответствуют сути дела... А что с тетраэдром? Эта задача, по характеру, совсем другая. И, на мой взгляд, совершенно замечательная, в некотором отношении... |
Не могу разобраться, какой итог обсуждения этой задачи (о сумму цифр числа 2^k, начало сообщение 175), но вот полезная ссылка.
__________________________
I love chess |
|
|
| номер сообщения: 49-2-3693 |
|
|
|
|
gennah: Навеяло:
http://en.wikipedia.org/wiki/Golomb_ruler |
Это явно улучшает оценку до 205. Интересно, предел ли это. |
|
|
| номер сообщения: 49-2-3694 |
|
|
|
|
iourique: gennah: Навеяло:
http://en.wikipedia.org/wiki/Golomb_ruler |
Это явно улучшает оценку до 205. Интересно, предел ли это. |
Трудно сказать... Вроде минимизировать сумму двух последних чисел в голову пока никому не приходило.  Да даже если и приходило, то вряд ли это сильно влияет на сложность задачи. А сложность задачи такова, что ничего шибко умнее тупого перебора (если точнее, ничего умнее Constraint Programming) предложить как-то не получается. 
P.S. Мой комп уже три дня пыжится над в чём-то похожей задачкой, и останавливать его я пока не намерен. |
|
|
| номер сообщения: 49-2-3695 |
|
|
|
|
gennah: iourique: gennah: Навеяло:
http://en.wikipedia.org/wiki/Golomb_ruler |
Это явно улучшает оценку до 205. Интересно, предел ли это. |
Трудно сказать... Вроде минимизировать сумму двух последних чисел в голову пока никому не приходило. Да даже если и приходило, то вряд ли это сильно влияет на сложность задачи. А сложность задачи такова, что ничего шибко умнее тупого перебора (если точнее, ничего умнее Constraint Programming) предложить как-то не получается. |
Как выяснилось, мой дополнительный вопрос оказался не столь уж дурацким и нечто подобное уже рассматривалось в математике. Узнал о Golomb ruler. Спасибо.
Раз уж пошла столь бурная дискуссия, то я коротко напишу свое решение задачи. Пусть a(i,j) - стоимость билета из пункта i в пункт j. Рассмотрим теперь четыре города i, j, m, n. Соединим города i, j маршрутом содержащим все города, за исключением городов m и n. Этот маршрут можно замкнуть до кругового двумя способами: i-n-m-j и i-m-n-j. Используя свойство независимсти полной стоимости поездки от маршрута получаем соотношение
a(i,n)+a(n,m)+a(m,j)=a(i,m)+a(m,n)+a(n,j)
Так как стоимость билета туда и обратно одинакова, то a(n,m) справа и слева сокращаются
a(i,n)+a(m,j)=a(i,m)+a(n,j)
Отсюда следует, что функция a(i,j) всегда представима в виде (этот шаг доказательства я опускаю, так как элегантного вывода у меня нет)
a(i,j)=d(i)+d(j)
Дальнейшее решение сводится к подбору функции d(i). Я стартовал со значений d(1)=0, d(2)=1. Затем подбирал наименьшее возможное значение для d(3) так, чтобы все стоимости билетов a(i,j) были различными (i,j<4). Затем аналогично подбирал d(4) и так далее до d(13). Такой алгоритм дает следующие значения для d(i)
0 1 2 4 7 12 20 29 38 52 73 94 127
Отсюда максимальная стоимость билета 94+127=221. |
|
|
| номер сообщения: 49-2-3696 |
|
|
|
|
MikhailK:
Отсюда следует, что функция a(i,j) всегда представима в виде (этот шаг доказательства я опускаю, так как элегантного вывода у меня нет)
a(i,j)=d(i)+d(j). |
Достаточно положить
d(1)=(a(1,2)+a(1,3)-a(2,3))/2
d(j)=a(1,j)-d(1).
То, что при таком определении a(i,j)=d(i)+d(j), доказывается в две строчки. |
|
|
| номер сообщения: 49-2-3697 |
|
|
|
|
gennah: iourique: gennah: Навеяло:
http://en.wikipedia.org/wiki/Golomb_ruler |
Это явно улучшает оценку до 205. Интересно, предел ли это. |
Трудно сказать... Вроде минимизировать сумму двух последних чисел в голову пока никому не приходило. |
Надо еще отметить, что различные разности - более ограничительное условие, чем различные суммы. То есть, 205 получается из неправильной оптимизации более сложной задачи  . |
|
|
| номер сообщения: 49-2-3698 |
|
|
|
|
| iourique: Надо еще отметить, что различные разности - более ограничительное условие, чем различные суммы. То есть, 205 получается из неправильной оптимизации более сложной задачи . |
Нет, ну разности с суммами - это всё же одно и то же. Видимо, вы имеете в виду, что в этих 205 мы ещё берём в расчёт суммы вида a_i + a_i, а это для изначальной задачки немного лишнее. |
|
|
| номер сообщения: 49-2-3699 |
|
|
|
|
| gennah:Видимо, вы имеете в виду, что в этих 205 мы ещё берём в расчёт суммы вида a_i + a_i, а это для изначальной задачки немного лишнее. |
Именно это. |
|
|
| номер сообщения: 49-2-3700 |
|
|
|
|
Воспоминания о Мехмате - Шафаревич, Арнольд, Новиков ...
http://www.math.ru/lib/files/pdf/mehmat/mm3.pdf |
|
|
| номер сообщения: 49-2-3701 |
|
|
|
|
iourique: | dimarko:В чем фокус-то, товарищи математики? |
Отличное наблюдение. Фокус в том, что пары 1 и 9, 2 и 8, 3 и 7, 4 и 6 будут парами противоположных точек на любом маршруте (включая маршруты коня). А сумма чисел в каждой паре - 10. А любое 8-значное число, у которого суммы 1 и 5 цифры, 2 и 6 цифры, 3 и 7 цифры и 4 и 8 цифры равны, делится на 1111. |
Спасибо! Про суммы чисел мог бы и сам догадаться  . Не хотел, видимо, по указанным ранее причинам |
|
|
| номер сообщения: 49-2-3702 |
|
|
|
|
А вот у кого есть под рукой Градштейн-Рыжик?
Или где найти его в сети?
Мне нужен параграф с действиями над степенными рядами -
там у меня вопрос к знатокам мат.анализа 
А впрочем, можно и так задать.
Там (и во многих других учебниках, справочниках и т.п.)
есть формула возведения степенного ряда в степень n
и подчеркивается, что n - целое число!!
А теперь, внимание, вопрос
а что если n - рациональная дробь?
Мой ответ: формула остается верной!
А Вы как думаете?
__________________________
I love chess |
|
|
| номер сообщения: 49-2-3766 |
|
|
|
|
zak06: А вот у кого есть под рукой Градштейн-Рыжик?
Или где найти его в сети?
Мне нужен параграф с действиями над степенными рядами -
там у меня вопрос к знатокам мат.анализа |
Этот кирпич у меня всегда под рукой. В сети наверняка есть. |
|
|
| номер сообщения: 49-2-3767 |
|
|
|
|
zak06:
есть формула возведения степенного ряда в степень n
и подчеркивается, что n - целое число!!
А теперь, внимание, вопрос
а что если n - рациональная дробь?
Мой ответ: формула остается верной!
А Вы как думаете? |
Да это же просто как бином Ньютона! Пожалуй никакого отличия быть не должно. Только биномиальные коэффиценты нужно правильно заменить на соответствующие множители составленные из Гамма функций.
А зачем требование рациональности n? Выглядит так, что n вообще может быть любым.
PS В Градштейне-Рыжике написана формула идентичная формуле Power series raised to powers |
|
|
| номер сообщения: 49-2-3768 |
|
|
|
|
Переполняют чувства в связи с игрой ЧтоГдеКогда. А где такое обсуждается?
__________________________
ИМХО |
|
|
| номер сообщения: 49-2-3796 |
|
|
|
|
Grigoriy: Воспоминания о Мехмате - Шафаревич, Арнольд, Новиков ...
http://www.math.ru/lib/files/pdf/mehmat/mm3.pdf |
Задачу номер два у Арнольда (из олимпиады для дошкольников со страницы номер 28) решал минут 15. Минут через 10 придумал решение, опасное для жизни альпиниста (решение встречено диким хохотом всех домашних), я бы лучше на скале остался. А еще через 5 минут задача для дошкольников была решена. |
|
|
| номер сообщения: 49-2-3798 |
|
|
|
|
| Игорь: Переполняют чувства в связи с игрой ЧтоГдеКогда. А где такое обсуждается? |
здесь |
|
|
| номер сообщения: 49-2-3799 |
|
|
|
|
MikhailK: zak06:
есть формула возведения степенного ряда в степень n
и подчеркивается, что n - целое число!!
А теперь, внимание, вопрос
а что если n - рациональная дробь?
Мой ответ: формула остается верной!
А Вы как думаете? |
Да это же просто как бином Ньютона! Пожалуй никакого отличия быть не должно. Только биномиальные коэффиценты нужно правильно заменить на соответствующие множители составленные из Гамма функций.
А зачем требование рациональности n? Выглядит так, что n вообще может быть любым.
PS В Градштейне-Рыжике написана формула идентичная формуле Power series raised to powers |
Запись выражения для коэффициентов степени ряда
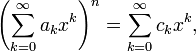
в виде рекуррентных соотношений
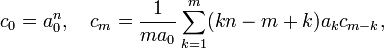
мне показалась не совсем тривиальной. Мне не сразу удалось придумать простой вывод этого соотношения. Из вывода следует, что степень n может быть совершенно произвольным числом. |
|
|
| номер сообщения: 49-2-3813 |
|
|
|
|
MikhailK: MikhailK: zak06:
есть формула возведения степенного ряда в степень n
и подчеркивается, что n - целое число!!
А теперь, внимание, вопрос
а что если n - рациональная дробь?
Мой ответ: формула остается верной!
А Вы как думаете? |
Да это же просто как бином Ньютона! Пожалуй никакого отличия быть не должно. Только биномиальные коэффиценты нужно правильно заменить на соответствующие множители составленные из Гамма функций.
А зачем требование рациональности n? Выглядит так, что n вообще может быть любым.
PS В Градштейне-Рыжике написана формула идентичная формуле Power series raised to powers |
Запись выражения для коэффициентов степени ряда
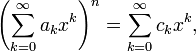
в виде рекуррентных соотношений
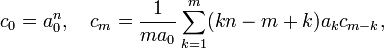
мне показалась не совсем тривиальной. Мне не сразу удалось придумать простой вывод этого соотношения. Из вывода следует, что степень n может быть совершенно произвольным числом. |
Вот моя заметка, в к-й я (и мой со-автор, и рецензент!) не обратили внимания, что формула верна для целых n.
Уже после опубликования я забеспокоился и после некоторых усилий я убедил себя, что я знаю, что она верна и для n вида m/n.
А любопытно увидеть Ваш вывод.
Что касается иррациональных n, то каждый математик, с к-м я пытался обсуждать это, в первую очередь говорил, что он не понимает, что значит ряд в степени pi, тогда как для физика (как я) это вообще не проблема - хоть возводи в степень I -
а кстати, что получится, если возвести самый простой ряд, да хотя бы 1+q+q^2+q^3+..., в степень I?
__________________________
I love chess |
|
|
| номер сообщения: 49-2-3858 |
|
|
|
|
zak06:
...а кстати, что получится, если возвести самый простой ряд, да хотя бы 1+q+q^2+q^3+..., в степень I? |
В качестве "оправдания" последнего вопроса (придумал только что!):
| Любопытен не порок, а большое свинство(С) |
__________________________
I love chess |
|
|
| номер сообщения: 49-2-3859 |
|
|
|
|
| zak06: что получится, если возвести самый простой ряд, да хотя бы 1+q+q^2+q^3+..., в степень I? |
Что такое I, i = (-1)^1/2? А как поднимать бесконечный ряд в любую степень? |
|
|
| номер сообщения: 49-2-3861 |
|
|
|
|
Хайдук: | zak06: что получится, если возвести самый простой ряд, да хотя бы 1+q+q^2+q^3+..., в степень I? |
Что такое I, i = (-1)^1/2? А как поднимать бесконечный ряд в любую степень? |
А это и есть мой (а теперь и Ваш ) вопрос.
__________________________
I love chess |
|
|
| номер сообщения: 49-2-3862 |
|
|
|
|
| zak06: А любопытно увидеть Ваш вывод. |
Нет проблем. Пусть функция f(z) и её p-ая степень имеют следующие разложения в ряд
нам необходимо связать между собой коэффициенты в этих разложениях. Для этого рассмотрим также ряды для производных
Теперь необходимые соотношения между коэффициентами получаются, если в элементарное соотношение
подставить выписанные выше разложения и собрать коэффициенты при одинаковых степенях z.
zak06:
Что касается иррациональных n, то каждый математик, с к-м я пытался обсуждать это, в первую очередь говорил, что он не понимает, что значит ряд в степени pi, тогда как для физика (как я) это вообще не проблема - хоть возводи в степень I -
а кстати, что получится, если возвести самый простой ряд, да хотя бы 1+q+q^2+q^3+..., в степень I? |
А какая проблема с возведением в произвольную степень? Например, есть такая функция, как экспонента. Вы её также боитесь?
Как известно, выражение a^b (a в степени b) необходимо понимать как e^(b*ln(a)). Так как логарифм является многозначной функцией, то и операция возведения в степень при нецелом b является многозначной. Никакой трагедии я тут не вижу.
Что касается возведения ряда 1+q+q^2+q^3+..., в степень I, то я не вижу, что бы могло помешать использовать приведенные ранее рекуррентные соотношения. Ясно, что при выборе определенной ветви логарифма значения коэффициентов разложения будут обычными комплексными числами. В чем тут проблема? |
|
|
| номер сообщения: 49-2-3871 |
|
|
|
|
| MikhailK: Как известно, выражение a^b (a в степени b) необходимо понимать как e^(b*ln(a)). Так как логарифм является многозначной функцией, то и операция возведения в степень при нецелом b является многозначной. |
Многозначность не всплывает ли только в комплексной области? |
|
|
| номер сообщения: 49-2-3894 |
|
|
|
|
Хайдук: | MikhailK: Как известно, выражение a^b (a в степени b) необходимо понимать как e^(b*ln(a)). Так как логарифм является многозначной функцией, то и операция возведения в степень при нецелом b является многозначной. |
Многозначность не всплывает ли только в комплексной области? |
Это зависит от личных предпочтений. Дело в том, что натуральный логарифм является многозначной функцией даже для вещественного аргумента. Другое дело, что в случае вещественного и положительного аргумента обычно по умолчанию выбирают ту ветвь, которая дает вещественное значение для логарифма.
В нашем случае удобнее считать иначе и всегда рассматривать логарифм как многозначную функцию. В этом случае никаких проблем с возведением ряда в комплексную степень нет, ну или я их в упор не вижу. |
|
|
| номер сообщения: 49-2-3895 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|
