|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Ну, я так не играю... Там даже объяснили все, а я три дня мучался. |
|
|
| номер сообщения: 49-2-3163 |
|
|
|
|
iourique:
Ну, я так не играю... Там даже объяснили все, а я три дня мучался. |
Там ещё статья упоминается
Bankoff, L. and Garfunkel, J. "The Heptagonal Triangle." Math. Mag. 46, 7-19, 1973.
Я её глянул по диагонали. Там цела россыпь подобных соотношений. Желающим могу её прислать.
Есть ещё аналогичные соотношения для углов кратных Pi/9
http://mathworld.wolfram.com/TrigonometryAnglesPi9.html
А вот ещё тождество
 |
|
|
| номер сообщения: 49-2-3164 |
|
|
|
|
вообще
 |
|
|
| номер сообщения: 49-2-3166 |
|
|
|
|
iourique: вообще
|
человека неподготовленного такое обобщение может несколько смутить)) |
|
|
| номер сообщения: 49-2-3168 |
|
|
|
|
| номер сообщения: 49-2-3169 |
|
|
|
|
| Классика: на какое минимальное количество частей надо разрезать равносторонний треугольник, чтобы из него можно было сложить квадрат? |
|
|
| номер сообщения: 49-2-3176 |
|
|
|
|
| azur: Классика: на какое минимальное количество частей надо разрезать равносторонний треугольник, чтобы из него можно было сложить квадрат? |
Я получил решение о разрезе на 5 частей.
Ставим равнолицевой квадрат на одной из сторон треугольника(симметрично).Разрез производим по сторон квадрата,а верхнего треугольника разрезаем и по линии симетрии (медиана).Получаем 5 частей - шестиугольник плюс две пары прямоугольных треугольников.
Доказательсто несложное , но весьма длинное ... А возможно ли уменшит частей ? Пока не вижу как... |
|
|
| номер сообщения: 49-2-3178 |
|
|
|
|
Всё, я сдался. Как обычно, Google знает ответы на все вопросы.
Haberdasher's puzzle
Выходит, что при таком выворачивании наизнанку треугольника получается квадрат и наоборот.  |
|
|
| номер сообщения: 49-2-3179 |
|
|
|
|
| номер сообщения: 49-2-3196 |
|
|
|
|
Одна из задач Арнольда формулируется следующим образом
| Можно ли из рубля сложить плоскую фигуру с большим периметром? |
На самом деле вопрос поставлен не совсем корректно и ответ зависит от того, что понимать под операцией складывания.
1) Если под складыванием понимать последовательность перегибаний, то ответ отрицательный.
2) Если же разрешить отгибать загнутые части, то ответ неизвестен.
Эти факты я знал. Однако сегодня я обнаружил статью, где показано, что ответ может быть и положительным. Если разрешить складывать лист сразу по нескольким линиям одновременно (без растяжений), то, как оказалось, периметр можно сделать сколь угодно большим.
Об этом можно почитать в этой популярной статье. Мне понравилось.
А. Петрунин
Плоское оригами и длинный рубль. |
|
|
| номер сообщения: 49-2-3197 |
|
|
|
|
Пропущен один член "последовательности"  :
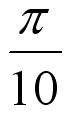
Это число тоже заслуживает внимания:
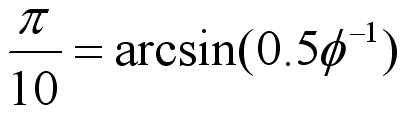
где ф - золотое сечение.
Кстати, задача: выведите эту формулу.  |
|
|
| номер сообщения: 49-2-3206 |
|
|
|
|
ygeshelin:
Пропущен один член "последовательности" :
|
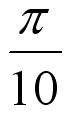Если в моей ссылке заменить 9 на 10 (или на 5), то неожиданно появится страничка с ответом.
А если серьёзно, то вычислимость тригонометрических функций в радикалах для угла pi/10 мне известна со школы. У Сканави наверняка есть дюжина задачек на эту тему. |
|
|
| номер сообщения: 49-2-3207 |
|
|
|
|
Утверждения Теории чисел часто формулируются очень просто, а доказательство их бывает весьма затруднительно. Классический пример - Великая теорема Ферма.
Есть две гипотезы: одна о том, что любое четное число представимо в виде суммы двух простых; другая о том, что любое нечетное число представимо в виде суммы трех простых. Кто и что знает по этому поводу? В частности, по поводу того, как "коррелируют" между собой два этих утверждения.
|
|
|
| номер сообщения: 49-2-3228 |
|
|
|
|
| Sad_Donkey:Есть две гипотезы: одна о том, что любое четное число представимо в виде суммы двух простых; другая о том, что любое нечетное число представимо в виде суммы трех простых. Кто и что знает по этому поводу? В частности, по поводу того, как "коррелируют" между собой два этих утверждения. |
Моих знаний хватает только на то, чтобы дать ссылку на проблему Гольдбаха |
|
|
| номер сообщения: 49-2-3229 |
|
|
|
|
MikhailK: | Sad_Donkey:Есть две гипотезы: одна о том, что любое четное число представимо в виде суммы двух простых; другая о том, что любое нечетное число представимо в виде суммы трех простых. Кто и что знает по этому поводу? В частности, по поводу того, как "коррелируют" между собой два этих утверждения. |
Моих знаний хватает только на то, чтобы дать ссылку на проблему Гольдбаха |
Спасибо за то, что откликнулись и за ссылку. С ее помощью можно добраться до списка известных нерешенных проблем (в том числе - математических). Жалко, что нет прайс-листа...
Сейчас математика меня больше интересует "как философия". (Таким же образом может интересовать и физика или химия).
Простые числа - стоит ли за ними какая-то "философия"? Являются ли они какими-то особенными, базисными, что ли. Разложение на простые множители, в этом смысле, мало интересно. Важен ли или что объясняет тот факт, что любое четное число может быть представлено в виде суммы двух простых?
Изощренность человеческого ума при доказательства математических утверждений, просто поражает! Но достижения его кажутся иногда чисто "спортивными" и просто жаль потраченного потенциала...
|
|
|
| номер сообщения: 49-2-3230 |
|
|
|
|
Sad_Donkey: Жалко, что нет прайс-листа...
|
Ну почему же, имеется. Этот прайс лист на слуху, но уверен, что есть и ещё несколько.
| Sad_Donkey:Простые числа - стоит ли за ними какая-то "философия"? Являются ли они какими-то особенными, базисными, что ли. Разложение на простые множители, в этом смысле, мало интересно. |
Свойства простых чисел удивительным образом цепляются за некоторые вполне не теоретикочисловые проблемы. Например распределение простых чисел тесно связано с гипотезой Римана, а от справедливости гипотезы Римана вообще зависит огромное количество математических утверждений.
Sad_Donkey:
Важен ли или что объясняет тот факт, что любое четное число может быть представлено в виде суммы двух простых? |
Где-то я читал, что сложность подобных проблем связана с тем, что простые числа характеризуют свойства чисел относительно перемножения, но при этом в проблеме Гольдбаха интересуются их свойствами относительно сложения. Конкретно эта проблема может и совершенно неважна для математики (как и теорема Ферма), но всегда приговаривают, что попытки решения могут дать толчок новым разделам математики.
PS Мне, как физику, совершенно непонятна суета вокруг гипотезы Римана. Совершенно ясно, что если первый триллион нетривиальных нулей имеет мнимую часть равную 0.5, то отсюда сразу следует, что и все остальные нетривиальные нули обладают таким свойством. |
|
|
| номер сообщения: 49-2-3231 |
|
|
|
|
| MikhailK: Свойства простых чисел удивительным образом цепляются за некоторые вполне не теоретикочисловые проблемы. Например распределение простых чисел тесно связано с гипотезой Римана, а от справедливости гипотезы Римана вообще зависит огромное количество математических утверждений. |
Я в философии не силён, но по-моему это "удивительным образом" притянуто за уши. Это скорее гипотеза Римана теоретикочисловая. 
| MikhailK: PS Мне, как физику, совершенно непонятна суета вокруг гипотезы Римана. Совершенно ясно, что если первый триллион нетривиальных нулей имеет мнимую часть равную 0.5, то отсюда сразу следует, что и все остальные нетривиальные нули обладают таким свойством. |
Конечно, це ж математическая индукция.
В принципе, уже давно накопилась уйма статей с утверждениями "Если гипотеза Римана справедливо, то... [собственно теорема]" Аналогично: "Если P не равно NP, то... [собственно теорема]"
В общем, математики тоже убедили себя, что и то, и другое верно - осталось просто доказать. Ну а так как на данный момент доказательства нет, приходится вставлять эти "если" - для формальности, так сказать. |
|
|
| номер сообщения: 49-2-3232 |
|
|
|
|
| Спасибо, Михаил. Сообщенные вами сведения вдохновляют меня поработать остатками мозгов. (При случае, на процент претендуете?). Но гипотезой Берча и Свиннертона — Дайера я заниматься не стану, конечно. Уж очень мне эти фамилии не нравятся - каждая в отдельности и, тем более, в коллекции. Наверное, придется заняться "P и NP" - деньги нужны... Очень заинтересовало ваше "мне, как физику". Известно, что физики и математики по-разному смотрят на мир, как раз, в филисофском плане...
|
|
|
| номер сообщения: 49-2-3233 |
|
|
|
|
| Sad_Donkey:Очень заинтересовало ваше "мне, как физику". Известно, что физики и математики по-разному смотрят на мир, как раз, в филисофском плане... |
Есть стандартный способ отличить физика от математика. Если ученый не смог прочитать третий том Ландавшица дальше первой главы, то он математик. Эти странные математики ни во что не ставят этот десятитомный курс теоретической физики. А вот среди физиков, он наоборот считается настольной библией. |
|
|
| номер сообщения: 49-2-3234 |
|
|
|
|
gennah:Я в философии не силён, но по-моему это "удивительным образом" притянуто за уши. Это скорее гипотеза Римана теоретикочисловая.
|
Математикам виднее. Я на дзета-функцию Римана смотрю как на очередную спецфункцию и у меня она с теорией чисел связана слабо. |
|
|
| номер сообщения: 49-2-3235 |
|
|
|
|
| MikhailK:Математикам виднее. Я на дзета-функцию Римана смотрю как на очередную спецфункцию и у меня она с теорией чисел связана слабо. |
Скорее, не сама дзета-функция, а гипотеза о её нулях связана. Она как раз и эквивалентна утверждению о распределении простых чисел.
В общем, что-то вроде ещё одной хитрой функции, которая несёт в себе скрытую информацию. Ну например, по внешнему виду Гамма-функции не сразу скажешь, что там скрыт факториал (конечно, увидеть это не так и сложно, но всё-таки), да и не особо оно нужно порой. Или функция Эйлера, которая вдруг ни с того, ни с сего содержит информацию о числе разбиений. А на вид - функция, да и функция. Мало ли по какому ещё поводу она возникнуть может?..
Такой вот у меня взгляд на это дело...  А может, просто настроение такое. |
|
|
| номер сообщения: 49-2-3236 |
|
|
|
|
Sad_Donkey: Утверждения Теории чисел часто формулируются очень просто, а доказательство их бывает весьма затруднительно. Классический пример - Великая теорема Ферма.
Есть две гипотезы: одна о том, что любое четное число представимо в виде суммы двух простых; другая о том, что любое нечетное число представимо в виде суммы трех простых. Кто и что знает по этому поводу? В частности, по поводу того, как "коррелируют" между собой два этих утверждения.
|
из 1-ого очевидно следует 2-ое. А вот из 2-ого 1-ое мне сразу не видно.
Что касается связи дзеты с теорией чисел она очевидна:
(1-1/р1)(1-1/р2)...(1-1/р(n)) - это то, что остаётся в натуральном ряду когда выбросим всё, делящееся на первые n простых. Беря обратное этому произведению и произведя перемножение, получаем дзету - ввиду однозначности разложения натуральных чисел в произведение простых |
|
|
| номер сообщения: 49-2-3237 |
|
|
|
|
Sad_Donkey: [
Изощренность человеческого ума при доказательства математических утверждений, просто поражает! Но достижения его кажутся иногда чисто "спортивными" и просто жаль потраченного потенциала...
|
Вы прямо цитируете Льва Николаича :-)
"Главное же то, что вопрос мой личный: что я такое с моими желаниями? --
оставался уже совсем без ответа. И я понял, что знания эти очень интересны,
очень привлекательны, но что точны и ясны эти знания обратно пропорционально
их приложимости к вопросам жизни: чем менее они приложимы к вопросам жизни,
тем они точнее и яснее, чем более они пытаются давать решения на вопросы
жизни, тем более они становятся неясными и непривлекательными. Если
обратишься к той отрасли этих знаний, которые пытаются давать решения на
вопросы жизни, -- к физиологии, психологии, биологии, социологии, -- то тут
встречаешь поражающую бедность мысли, величайшую неясность, ничем не
оправданную притязательность на решение неподлежащих вопросов и
беспрестанные противоречия одного мыслителя с другими и даже с самим собою.
Если обратишься к отрасли знаний, не занимающихся разрешением вопросов
жизни, но отвечающих на свои научные, специальные вопросы, то восхищаешься
силой человеческого ума, но знаешь вперёд, что ответов на вопросы жизни нет.
Эти знания прямо игнорируют вопрос жизни. Они говорят: "На то, что ты такое
и зачем ты живёшь, мы не имеем ответов и этим не занимаемся; а вот если тебе
нужно знать законы света, химических соединений, законы развития организмов,
если тебе нужно знать законы тел, их форм и отношение чисел и величин, если
тебе нужно знать законы своего ума, то на всё это у нас есть ясные, точные и
несомненные ответы"." |
|
|
| номер сообщения: 49-2-3238 |
|
|
|
|
Grigoriy: Sad_Donkey:
Есть две гипотезы: одна о том, что любое четное число представимо в виде суммы двух простых; другая о том, что любое нечетное число представимо в виде суммы трех простых. Кто и что знает по этому поводу? В частности, по поводу того, как "коррелируют" между собой два этих утверждения.
|
из 1-ого очевидно следует 2-ое. А вот из 2-ого 1-ое мне сразу не видно.
|
Оно и не следует. Более того, второе доказано для достаточно больших чисел (это результат Виноградова), а первое - нет. |
|
|
| номер сообщения: 49-2-3239 |
|
|
|
|
Сэд, Григорий, а скажите, разве, скажем, элементы линейной алгебры, основы математического анализа не помогают в решении физических и экономических задач, которые жизнь ставит перед чедовеком?
Для чего живём, Лев Николаевич? А вот часть самых умных людей и живёт для того, чтоб открывать "числовые соответствия", брать явления природыв формулы. И больше двигать жизнь, чем поиск смысла жизни. А для чего живёт и решает Григорий, который Перельман? |
|
|
| номер сообщения: 49-2-3240 |
|
|
|
|
iourique: Grigoriy: Sad_Donkey:
Есть две гипотезы: одна о том, что любое четное число представимо в виде суммы двух простых; другая о том, что любое нечетное число представимо в виде суммы трех простых. Кто и что знает по этому поводу? В частности, по поводу того, как "коррелируют" между собой два этих утверждения.
|
из 1-ого очевидно следует 2-ое. А вот из 2-ого 1-ое мне сразу не видно.
|
Оно и не следует. Более того, второе доказано для достаточно больших чисел (это результат Виноградова), а первое - нет. |
Да, все так.
|
|
|
| номер сообщения: 49-2-3241 |
|
|
|
|
| gennah: не сама дзета-функция, а гипотеза о её нулях связана. Она как раз и эквивалентна утверждению о распределении простых чисел. |
Что за распределение такое? Что будет с распределением, если гипотеза Римана окажется неверной? |
|
|
| номер сообщения: 49-2-3243 |
|
|
|
|
Хайдук: | gennah: не сама дзета-функция, а гипотеза о её нулях связана. Она как раз и эквивалентна утверждению о распределении простых чисел. |
Что за распределение такое? Что будет с распределением, если гипотеза Римана окажется неверной? |
Да что-то вроде уточнения теоремы о простых числах...
Ну а что будет? Да ничего не будет - будем живы, не помрём. |
|
|
| номер сообщения: 49-2-3245 |
|
|
|
|
| номер сообщения: 49-2-3258 |
|
|
|
|
Ну и правильно сделали. Сами туда перенесетесь(частично)?
|
|
|
| номер сообщения: 49-2-3269 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|
