|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
По-видимому, процесс сходится всегда, но наверное бывает и наилучшая стратегия с наименьшим из наибольших чисел ходов  |
|
|
| номер сообщения: 49-2-3035 |
|
|
|
|
Хайдук: По-видимому, процесс сходится всегда, но наверное бывает и наилучшая стратегия с наименьшим из наибольших чисел ходов  |
Минимизировать в этой задаче, вроде, неинтересно... |
|
|
| номер сообщения: 49-2-3036 |
|
|
|
|
Может быть - черт не дремлет  |
|
|
| номер сообщения: 49-2-3037 |
|
|
|
|
Найти 48 после запятой знак числа
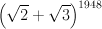 . .
Калькуляторами пользоваться нечестно. |
|
|
| номер сообщения: 49-2-3040 |
|
|
|
|
| iourique: Минимизировать в этой задаче, вроде, неинтересно... |
А максимальное решение известно кому-либо?  |
|
|
| номер сообщения: 49-2-3041 |
|
|
|
|
Хайдук: | iourique: Минимизировать в этой задаче, вроде, неинтересно... |
А максимальное решение известно кому-либо?  |
Кому-то - да. Для простого случая, примером кого-то являюсь я; в сложном случае, я, кажется, знаю ответ, но доказать пока не получается. |
|
|
| номер сообщения: 49-2-3042 |
|
|
|
|
Вброшу еще одну задачку с того же сайта:
Дано число n такое, что число 2n-1 состоит из тех же цифр, что и n, но в другом порядке (например, 37 и 73). Доказать, что если число n кончается на 3, то оно содержит цифру 8. |
|
|
| номер сообщения: 49-2-3043 |
|
|
|
|
iourique: Найти 48 после запятой знак числа
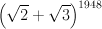 . .
Калькуляторами пользоваться нечестно. |
Подглядел ответ. Вроде все делал правильно, а вот до главной идеи додуматься не смог. |
|
|
| номер сообщения: 49-2-3056 |
|
|
|
|
| Пока решения не вносите, у меня ещё не было времени подумать. |
|
|
| номер сообщения: 49-2-3057 |
|
|
|
|
iourique: Вброшу еще одну задачку с того же сайта:
Дано число n такое, что число 2n-1 состоит из тех же цифр, что и n, но в другом порядке (например, 37 и 73). Доказать, что если число n кончается на 3, то оно содержит цифру 8. |
А вот эту задачу удалось раскрутить самостоятельно. Вот только пример подобного числа я пока не построил.
Ой, нашёл дыру в своих рассуждениях. |
|
|
| номер сообщения: 49-2-3058 |
|
|
|
|
| MikhailK: Вот только пример подобного числа я пока не построил. |
А я даже не искал. Математик, что сказать... Поискал теперь: 173945683 и 347891365. Интересно, можно ли короче. |
|
|
| номер сообщения: 49-2-3061 |
|
|
|
|
| iourique: Кому-то - да. Для простого случая, примером кого-то являюсь я |
Эта верхняя граница близка к точной?  |
|
|
| номер сообщения: 49-2-3063 |
|
|
|
|
iourique: | MikhailK: Вот только пример подобного числа я пока не построил. |
А я даже не искал. Математик, что сказать... Поискал теперь: 173945683 и 347891365. Интересно, можно ли короче. |
Можно. Есть много пар чисел, меньших приведенной Вами. Вот первые 50 пар:
158743 317485
185743 371485
415873 831745
418573 837145
1508743 3017485
1540873 3081745
1574893 3149785
1587043 3174085
1587403 3174805
1587493 3174985
1589473 3178945
1589743 3179485
1594873 3189745
1598743 3197485
1708543 3417085
1740853 3481705
1745893 3491785
1748593 3497185
1850743 3701485
1854073 3708145
1857043 3714085
1857403 3714805
1857493 3714985
1859473 3718945
1859743 3719485
1870543 3741085
1874053 3748105
1874593 3749185
1894573 3789145
1895743 3791485
1945873 3891745
1948573 3897145
1958743 3917485
1985743 3971485
4015873 8031745
4018573 8037145
4051873 8103745
4071853 8143705
4085173 8170345
4087153 8174305
4150873 8301745
4158703 8317405
4158973 8317945
4159873 8319745
4170853 8341705
4185073 8370145
4185703 8371405
4185973 8371945
4187053 8374105
4189573 8379145 |
|
|
| номер сообщения: 49-2-3064 |
|
|
|
|
Раз пошла такая пьянка, опубликую следующие 50:
4195873 8391745
4198573 8397145
4571893 9143785
4587193 9174385
4589173 9178345
4591873 9183745
4715893 9431785
4718593 9437185
4857193 9714385
4859173 9718345
4871593 9743185
4891573 9783145
4915873 9831745
4918573 9837145
15008743 30017485
15040873 30081745
15074893 30149785
15087043 30174085
15087403 30174805
15087493 30174985
15089473 30178945
15089743 30179485
15094873 30189745
15098743 30197485
15400873 30801745
15408703 30817405
15408973 30817945
15409873 30819745
15470893 30941785
15487093 30974185
15489073 30978145
15490873 30981745
15673843 31347685
15674383 31348765
15683743 31367485
15684373 31368745
15687343 31374685
15687433 31374865
15704893 31409785
15736843 31473685
15743683 31487365
15748903 31497805
15748993 31497985
15749893 31499785
15836743 31673485
15843673 31687345
15867343 31734685
15867433 31734865
15870043 31740085
15870403 31740805 |
|
|
| номер сообщения: 49-2-3065 |
|
|
|
|
ygeshelin: iourique: | MikhailK: Вот только пример подобного числа я пока не построил. |
А я даже не искал. Математик, что сказать... Поискал теперь: 173945683 и 347891365. Интересно, можно ли короче. |
Можно. Есть много пар чисел, меньших приведенной Вами. |
Спасибо. |
|
|
| номер сообщения: 49-2-3066 |
|
|
|
|
Хайдук: | iourique: Кому-то - да. Для простого случая, примером кого-то являюсь я |
Эта верхняя граница близка к точной?  |
Я - нижняя граница, в данном случае. Она сильно неточна - решение знает еще много кто. |
|
|
| номер сообщения: 49-2-3067 |
|
|
|
|
Roger: Раз пошла такая пьянка, опубликую следующие 50:
|
В первых 50 миллионах натуральных чисел есть 544 числа n с таким свойством.
А в следующих 100 миллионах, между 50 000 000 и 150 000 000 - ни одного!
Обалденно скачкообразная функция. |
|
|
| номер сообщения: 49-2-3068 |
|
|
|
|
ygeshelin: Roger: Раз пошла такая пьянка, опубликую следующие 50:
|
В первых 50 миллионах натуральных чисел есть 544 числа n с таким свойством.
А в следующих 100 миллионах, между 50 000 000 и 150 000 000 - ни одного!
Обалденно скачкообразная функция. |
Если заметить, что с 5,6,7,8,9 такие числа начинаться не могут, становится чуть менее загадочно - мы говорим теперь об интервале от 100 до 150 миллионов. Надо заметить, что чисел, начинающихся с 10,11,12,13, или 14, в приведенных выше тоже нет. Хотя принципиально такие бывают, например, 125874158743. |
|
|
| номер сообщения: 49-2-3069 |
|
|
|
|
| iourique: Хотя принципиально такие бывают, например, 125874158743. |
Думаю. кстати, что число 125574188743 - минимальное, начинающееся с чего-то меньшего 15. |
|
|
| номер сообщения: 49-2-3070 |
|
|
|
|
Стащил из треда Старого Семена задачку
ААМН:
Теперь – совсем о другом. Задача по арифметике, которую задали моему брату на устном экзамене по математике при поступлении в Физтех в далёкие 60-ые годы.
Проезд в автобусе стоит 5 копеек, но ни у кого из пассажиров нет пятикопеечной монеты, однако у каждого есть неограниченное количество десяти-, пятнадцати- и двадцатикопеечных монет. Может ли при этом каждый расплатиться только за себя?
Подразумевается, что в автобусе находится более одного пассажира.
Вперёд, друзья! |
Достаточно показать, что смогут расплатиться группа из двух и трёх человек. Большее количество народу всегда можно разбить на двойки и тройки.
Задачка оказалась простой. У меня получилось, что можно.
А зачем двадцатикопеечные монеты? Мне они оказались не нужны. |
|
|
| номер сообщения: 49-2-3136 |
|
|
|
|
Вот такой шахматный латинский квадрат (каждая фигура по разу на вертикали и горизонтали).
У него есть две особенности: 1) симметрия относительно главной диагонали, 2) белый король на концах этой диагонали (a8 и h1).
Хотелось бы найти квадрат 9х9 с такими же свойствами. Кто-нибудь может помочь? :-) |
|
|
| номер сообщения: 49-2-3137 |
|
|
|
|
| azur:Хотелось бы найти квадрат 9х9 с такими же свойствами. Кто-нибудь может помочь? :-) |
Задача сводится к классификации квазигрупп порядка 9 с коммутативной операцией умножения. Думаю, что их не так много. Поговорю на следующей неделе об этом с алгебраистами. |
|
|
| номер сообщения: 49-2-3151 |
|
|
|
|
Скончался Мартин Гарднер, американский математик, автор любимых книг моего детства "Математические головоломки и развлечения", "Математические досуги" и др.  |
|
|
| номер сообщения: 49-2-3152 |
|
|
|
|
mickey: Скончался Мартин Гарднер, американский математик, автор любимых книг моего детства "Математические головоломки и развлечения", "Математические досуги" и др.  |
 Много раз перечитывал его книги. Много раз перечитывал его книги. |
|
|
| номер сообщения: 49-2-3153 |
|
|
|
|
| azur: Хотелось бы найти квадрат 9х9 с такими же свойствами. Кто-нибудь может помочь? :-) |
Не получится. Так как фигур 9, а картинка симметричная, каждая фигура должна хоть раз отметиться на диагонали. Но король там стоит дважды, значит, кому-то не хватит места. |
|
|
| номер сообщения: 49-2-3157 |
|
|
|
|
iourique: | azur: Хотелось бы найти квадрат 9х9 с такими же свойствами. Кто-нибудь может помочь? :-) |
Не получится. Так как фигур 9, а картинка симметричная, каждая фигура должна хоть раз отметиться на диагонали. Но король там стоит дважды, значит, кому-то не хватит места. |
Рассуждения не понял. В примере 8x8, которое предоставил azur, черная ладья ни разу не попала на диагональ. Как это соотносится с Вашими рассуждениями?
Как известно, латинский квадрат является таблицей умножения некоторой квазигруппы. Если предположить, что эта квазигруппа является группой, то сразу получаем, что требуемых квадратов с нечетной длиной стороны не существует. Дело в том, что из требования "белый король на концах диагонали" следует существование подгруппы порядка 2, а такие подгруппы бывают только у групп чётного порядка.
Отсюда следует, что если квадрат 9x9 существует, то ему соответствует какая-то нетривиальная квазигруппа. |
|
|
| номер сообщения: 49-2-3158 |
|
|
|
|
| MikhailK: В примере 8x8, которое предоставил azur, черная ладья ни разу не попала на диагональ. Как это соотносится с Вашими рассуждениями? |
Всего черных ладей - 9. Из-за симметрии под диагональю их столько же, сколько над диагональю. Значит, вне диагонали - четное число черных ладей. Значит, хотя бы одна - на диагонали. Все дело в четности. |
|
|
| номер сообщения: 49-2-3159 |
|
|
|
|
iourique: | MikhailK: В примере 8x8, которое предоставил azur, черная ладья ни разу не попала на диагональ. Как это соотносится с Вашими рассуждениями? |
Всего черных ладей - 9. Из-за симметрии под диагональю их столько же, сколько над диагональю. Значит, вне диагонали - четное число черных ладей. Значит, хотя бы одна - на диагонали. Все дело в четности. |
Все верно. Если сторона нечетная, из соображений симметрии каждая фигура на диагонали будет по разу. |
|
|
| номер сообщения: 49-2-3160 |
|
|
|
|
Мне тут подкинули смешную задачку - посчитать
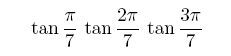 |
|
|
| номер сообщения: 49-2-3161 |
|
|
|
|
iourique: Мне тут подкинули смешную задачку - посчитать
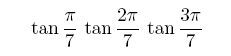 |
:) |
|
|
| номер сообщения: 49-2-3162 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2025 гг. |
|

|
|