|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Лачезар, давайте вернёмся к задаче про палатки. Я не вижу там больше подводных камней, а ответ, который получился и у iourique-а, и у меня Вы отвергли. Так где мы были неправы? |
|
|
| номер сообщения: 49-2-1824 |
|
|
|
|
LatchezarS: Придумайте шахматную партию , где после min (теоретически 16) ходов получим зту позицию.
Увь/ , много дуали - мн-о-о-ого.Но все йе интересно. |
Henry Ernest Dudeney
Leeds Mercury Supplement 07/1895
1.Кc3 d5 2.К:d5 Кc6 3.К:e7 g5 4.К:c8 Кf6 5.К:a7 Кe4 6.К:c6 Кc3 7.К:d8 Лg8 8.К:f7 Лg6 9.К:g5 Лe6 10.К:h7 Кb1 11.К:f8 Лa3 12.К:e6 b5 13.К:c7 Kрf7 14.К:b5 Kрg6 15.К:a3 Kрh5 16.К:b1 Kрh4
|
|
|
| номер сообщения: 49-2-1825 |
|
|
|
|
Правительство РФ учредило гранты молодым ученым
| Кандидаты наук, не достигшие 35 лет, смогут получить 600 тысяч рублей, а доктора наук моложе 40 лет - миллион рублей. Гранты рассчитаны на два года. Вице-премьер Сергей Иванов уточнил, что в общей сложности в 2009 году кандидаты наук смогут получить 400 грантов, а доктора наук - 60 грантов. Всего на выплату грантов в бюджете заложено 900 миллионов рублей. |
600000*400 + 1000000*60 = 300000000
900000000 - 300000000 = ?

Это вам не задачки решать! Тут серьезная проблема. |
|
|
| номер сообщения: 49-2-1826 |
|
|
|
|
MikhailK: 600000*400 + 1000000*60 = 300000000
900000000 - 300000000 = ? 
Это вам не задачки решать! Тут серьезная проблема. |
Хоть конкурс ответов проводи. |
|
|
| номер сообщения: 49-2-1827 |
|
|
|
|
| Напомнило анекдот о встрече двух бывших одноклассников (покупаю банку пива за доллар, продаю за три - вот на эти два процента и живу). Тут как раз этот самый случай - два процента чиновникам. |
|
|
| номер сообщения: 49-2-1828 |
|
|
|
|
| Формально несоответствия нет. В заголовке, и видимо Ивановым говорилось о грантах молодым учёным, а общая сумма - на все гранты. |
|
|
| номер сообщения: 49-2-1829 |
|
|
|
|
Король-самоубийца
На шахматной доске 1000*1000 стоит чёрный король и 499 белых ладей. Доказать, что как бы ни играли белые, король всегда может стать под удар одной из ладей |
|
|
| номер сообщения: 49-2-1861 |
|
|
|
|
Grigoriy: Король-самоубийца
На шахматной доске 1000*1000 стоит чёрный король и 499 белых ладей. Доказать, что как бы ни играли белые, король всегда может стать под удар одной из ладей |
Насилу решил, а выигрышная стратегия проста дальше некуда.... |
|
|
| номер сообщения: 49-2-1893 |
|
|
|
|
| Там психологическая ловушка - тpудно понять(мне во всяком случае было), что все пробития надо считать по отдельности |
|
|
| номер сообщения: 49-2-1894 |
|
|
|
|
| Grigoriy: Там психологическая ловушка - тpудно понять(мне во всяком случае было), что все пробития надо считать по отдельности |
У меня другие трудности были - я то по всем полям считал, то по всем путям, а надо было упрощать, упрощать и упрощать. |
|
|
| номер сообщения: 49-2-1895 |
|
|
|
|
Простенькая головоломка(я знаю 2 решения, чисто геометрическое и чисто алгебраическое):
Кубик 3х3х3 легко распилить 6 распилами на 27 кубиков. А каково минимальное число распилов, если части разрешается перекладывать перед распилами?
Распилы, понятно, только по плоскостям соединяющим кубики 1х1х1. |
|
|
| номер сообщения: 49-2-2046 |
|
|
|
|
drowsy: Простенькая головоломка(я знаю 2 решения, чисто геометрическое и чисто алгебраическое):
Кубик 3х3х3 легко распилить 6 распилами на 27 кубиков. А каково минимальное число распилов, если части разрешается перекладывать перед распилами?
Распилы, понятно, только по плоскостям соединяющим кубики 1х1х1. |
Я вроде решил. Где-то я видел эту задачу. Перельман? Гарднер?
А решение у меня тривиальное. Я даже затрудняюсь его назвать геометрическим или алгебраическим. |
|
|
| номер сообщения: 49-2-2047 |
|
|
|
|
| Ну я и не говорил, что задачка тяжёлая. Просто я решил геометрически, а жена чисто арифметически(тоже в 1-2 строчки, но совершенно по другому). Это фольклор, да. Откуда не знаю :) |
|
|
| номер сообщения: 49-2-2048 |
|
|
|
|
drowsy: Простенькая головоломка(я знаю 2 решения, чисто геометрическое и чисто алгебраическое):
Кубик 3х3х3 легко распилить 6 распилами на 27 кубиков. А каково минимальное число распилов, если части разрешается перекладывать перед распилами?
Распилы, понятно, только по плоскостям соединяющим кубики 1х1х1. |
Когда я вижу подобные задачки, то мне в голову лезут дурацкие мысли, навроде обобщения на случай куба произвольного размера.
Кстати, случай куба 4х4х4 легко решается (забавный ответ). Случай куба 5х5х5 мне в уме решить не удается. drowsy, работает ли твой геометрический или алгебраический метод в случае куба произвольного размера? |
|
|
| номер сообщения: 49-2-2050 |
|
|
|
|
Ну 4х4х4 это 6 распилов. Он содержит подкуб 3х3х3, значит меньше нельзя.
По первым прикидкам для nxnxn куба нужно 3*Х распилов,
где Х число распилов, нужных для одномерного блока длины n. То есть что-то похожее на док-во у меня есть,
но я его ещё не проверял, так что не уверен.
А решали мы так для n=3: Я просто посмотрел на центральный кубик. У него 6 граней, их все нужно пилить, значит 6 минимум. Можно даже представить упрощённую фигуру -- центральный кубик, к граням которого подклеено ещё 6 кубиков.
А жена решала так(Я её просто пытался сбить с толку, говоря, что 2^5>27, значит 5 должно быть достаточно, просто располагать нужно умнО.): В начале все распилы однозначны, после первого распила имеем два куска 9 и 18 кубиков. Даже если супер-умно пилить после 4 распилов из 1 куска можно получить только 16=2^4. Значит за 5 нельзя. А за 6 можно. |
|
|
| номер сообщения: 49-2-2052 |
|
|
|
|
| drowsy: Я просто посмотрел на центральный кубик. У него 6 граней, их все нужно пилить, значит 6 минимум. |
Блин, а мне это сразу в голову не пришло, старею. 
Просто поделил в уме на 9 и 18, потом бОльшие куски.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-2053 |
|
|
|
|
По первым прикидкам для nxnxn куба нужно 3*Х распилов,
где Х число распилов, нужных для одномерного блока длины n. |
Доказывается, вроде, так(шаг индукции): рассмотрим куб со стороной 2^{X-1}, находящийся внутри куба nxnxn так, что один угол у них совпадает. Тогда противоположный угол меньшего куба имеет дополнительно три (внешних)грани, которые придётся резать независимо. На внутренний куб нужно 3(X-1) разрезов, и ещё плюс три. Итого 3Х. |
|
|
| номер сообщения: 49-2-2055 |
|
|
|
|
drowsy:
По первым прикидкам для nxnxn куба нужно 3*Х распилов,
где Х число распилов, нужных для одномерного блока длины n. |
Доказывается, вроде, так(шаг индукции): рассмотрим куб со стороной 2^{X-1}, находящийся внутри куба nxnxn так, что один угол у них совпадает. Тогда противоположный угол меньшего куба имеет дополнительно три (внешних)грани, которые придётся резать независимо. На внутренний куб нужно 3(X-1) разрезов, и ещё плюс три. Итого 3Х. |
Здорово! Вроде получается тогда, что для многомерного куба ответ будет N*X, где N - размерность куба. |
|
|
| номер сообщения: 49-2-2056 |
|
|
|
|
| Ну бог с ней с многомерностью, главное, что на прямоугольники обобщается. То есть кубы тут ни при чём. Просто будет сумма из минимального числа разрезов для каждой стороны. |
|
|
| номер сообщения: 49-2-2058 |
|
|
|
|
drowsy:
По первым прикидкам для nxnxn куба нужно 3*Х распилов,
где Х число распилов, нужных для одномерного блока длины n. |
Доказывается, вроде, так(шаг индукции): рассмотрим куб со стороной 2^{X-1}, находящийся внутри куба nxnxn так, что один угол у них совпадает. Тогда противоположный угол меньшего куба имеет дополнительно три (внешних)грани, которые придётся резать независимо. На внутренний куб нужно 3(X-1) разрезов, и ещё плюс три. Итого 3Х. |
Что-то мне не нравится это доказательство - и индукция непонятно по чему, и, кажется, только оценка снизу доказывается.
По-моему, все проще - если я, конечно, ничего не упустил. Как ни режь прямоугольный параллелепипед произвольной размерности, получаешь два параллелепипеда, один из которых вкладывается в другой. Про меньший из двух, таким образом, можно просто забыть - все операции для него клонируются с большего. Задача - сделать больший кусок как можно меньше, т.е. уполовинить какую-нибудь сторону. Ответ - сумма округленных вверх двоичных логарифмов длин сторон. |
|
|
| номер сообщения: 49-2-2062 |
|
|
|
|
| drowsy: Ну бог с ней с многомерностью, главное, что на прямоугольники обобщается. То есть кубы тут ни при чём. Просто будет сумма из минимального числа разрезов для каждой стороны. |
Действительно! |
|
|
| номер сообщения: 49-2-2063 |
|
|
|
|
Что-то мне не нравится это доказательство - и индукция непонятно по чему, и, кажется, только оценка снизу доказывается.
|
Индукция, понятно, по Х. Oценкa сверху, вроде, тривиальна. Мне моё доказательство не нравится cовсем в другом месте: "дополнительно нужно резать три внешних грани". Тяжело классифицировать разрезы на "внутри меньшего куба или снаружи", когда части передвигаются.
Ваше аргумент гораздо лучше -- там вообще с этим проблем нет. |
|
|
| номер сообщения: 49-2-2064 |
|
|
|
|
| drowsy: Ну бог с ней с многомерностью, главное, что на прямоугольники обобщается. То есть кубы тут ни при чём. Просто будет сумма из минимального числа разрезов для каждой стороны. |
Выходит, что задача, в некотором смысле, тривиальная. Сначала режем прямоугольный параллелепипед вдоль одной из сторон, сдвигая получающиеся куски параллельным переносом. Аналогично рубим все в капусту вдоль других сторон. Обидно, что для достижения оптимального результата не нужно поворачивать отрезанные куски. Неужели эта дополнительная возможность не позволяет улучшить результат? |
|
|
| номер сообщения: 49-2-2071 |
|
|
|
|
| drowsy: Простенькая головоломка .. |
Сразу вспомнилось - как засунуть шесть блоков 1х2х2 в кубическую коробку 3х3х3? |
|
|
| номер сообщения: 49-2-2077 |
|
|
|
|
Однажды два приятеля - Толстый и Тонкий - решили сходить в пиццерию пообедать. Официант им принес разрезанную на две части пиццу
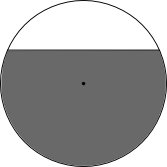
Так как Тонкий был не очень голоден, то больший кусок (содержит центр пиццы и закрашен серым) достался Толстому.
На следующий день они снова заглянули в ту же пиццерию. На этот раз им принесли пиццу разрезанную на четыре части
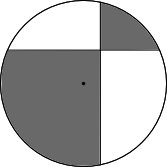
Приятели решили, что каждый возьмет куски через один (закрашенные серым или белым). Несложно доказать, что суммарная площадь серых кусков больше площади белых кусков.
На другой день им принесли пиццу разрезанную на шесть частей

Суммарная площадь каких кусков больше: белых или серых?
На следующий день им принесли пиццу разрезанную на восемь частей

Суммарная площадь каких кусков больше: белых или серых?
PS
1) Углы между разрезами равны.
2) Для простоты изложения я всегда предполагал, что серые кусочки содержат центр круга. |
|
|
| номер сообщения: 49-2-2141 |
|
|
|
|
В случае 6 частей - "серая" площадь больше "белой".
В случае 8 частей - площади одинаковы.
Если продолжить в том же духе, то на следующий день, при разделе пиццы на 10 частей, уже "белая" площадь (не содержащая центр) будет больше .. |
|
|
| номер сообщения: 49-2-2142 |
|
|
|
|
azur: В случае 6 частей - "серая" площадь больше "белой".
В случае 8 частей - площади одинаковы.
Если продолжить в том же духе, то на следующий день, при разделе пиццы на 10 частей, уже "белая" площадь (не содержащая центр) будет больше .. |
azur, ты знаешь простое доказательство в случае 10 частей?
А что будет в случае 14 частей?
Я смог самостоятельно разобраться в случае раздела пиццы на 2,4,6 и 8 частей. Остальное я честно подглядел в недавней работе. Если никто в ближайшее время не заинтересуется этой забавной геометрической задачей, то через несколько дней я дам ссылку на статью, где все эти вопросы обсуждаются. |
|
|
| номер сообщения: 49-2-2143 |
|
|
|
|
| номер сообщения: 49-2-2144 |
|
|
|
|
Повеселило начало статьи | Suppose you have a cake represented by the interval ([0, 1])... |
Которое в моем вольном переводе звучит так
| Предположим, что у вас есть торт, представленный отрезком [0, 1 ]... |
Сразу видно - математики.  |
|
|
| номер сообщения: 49-2-2145 |
|
|
|
|
MikhailK: azur, ты знаешь простое доказательство в случае 10 частей?
А что будет в случае 14 частей? |
В общем случае:
если центр пиццы находится на разрезе -
1) серая и белая площади будут равны при любом количестве разрезов (по соображениям симметрии)
если центр пиццы внутри серой области -
2) серая и белая площади равны только в случае четного количества разрезов N>2 или, что одно и то же, в случае когда количество разрезанных частей (2N>4) делится на 4.
3) если количество разрезов N = 1, 2 или 4k-1, серая площадь будет больше белой
4) если количество разрезов N = 4k+1, наоборот, серая площадь будет меньше .. |
|
|
| номер сообщения: 49-2-2146 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|