|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Roger: Меня возмущает совершенная оторванность этой задачи от жизни (т.е. от физики), которую я и попытался выразить, сославшись на Арнольда. |
Roger, простите, конечно, но, по-моему, сейчас именно Вы занимаетесь формализмом. Да, с точки зрения физики формулировка задачи не выдерживает критики - тут Вы очень убедительны. Но это не значит, что сама задача оторвана от жизни! Наверно, можно было бы придумать формулировку, которая бы Вас удовлетворила - эксперимент, при котором образец не подвергется вредному воздействию до определенного порогового уровня, а после него разрушается, приписать эксперименту и разрушенному образцу какую-нибудь цену и т.п. и т.д. Все это было бы очень здорово, но только отвлекало бы от задачи. Задача математической модели, как мне кажется, именно в том, чтобы абстрагировать какое-нибудь свойство и описать его, а уж потом адаптировать описание к реальной жизни. Иногда метод решения, какие-то идеи в решении важнее самого решения. Математику не стоит полностью отрывать от физики, но и путать с физикой не нужно. |
|
|
| номер сообщения: 49-2-1643 |
|
|
|
|
| Да я всё понимаю и даже соглашаюсь, просто не смог отказать себе в двойном удовольствии подразнить Григория и математиков. |
|
|
| номер сообщения: 49-2-1644 |
|
|
|
|
| Roger: Да я всё понимаю и даже соглашаюсь, просто не смог отказать себе в двойном удовольствии подразнить Григория и математиков. |
Что-то у меня с чувством юмора напряг наметился  . Извините. . Извините.
| ...Григория и математиков. |
А вот этого Григорий Вам не простит. |
|
|
| номер сообщения: 49-2-1645 |
|
|
|
|
Да какой из меня математик :-)
Я лично понял, что надо решать обратную(что кстати моментально даёт решение для случая n шариков) когда попытался кратко и понятно обьяснить решение товарищу.
Юрик, посмотрите личку. |
|
|
| номер сообщения: 49-2-1646 |
|
|
|
|
LatchezarS: Mатч Топалов - Камский
Моя "простенкая" задача:
|
Лачезар, несколько вопросов:
1) может ли часть быть (а) неодносвязной, как кони, или (б) связанной только через угол, как короли в следующем решении:
2) может ли часть зеркально отображаться (т.е. переворачиваться в 3-х мерном пространстве, а не только в плоскости), как случилось с конями на следующей диаграмме:
3) что считается решением - разрезка или сборка? Другими словами, если два варианта отличаются только перестановкой двух одинаковых деталей в сборке, следует ли считать их за один:
4) принимаются ли компьютерные решения? |
|
|
| номер сообщения: 49-2-1647 |
|
|
|
|
Grigoriy: Да какой из меня математик :-)
Я лично понял, что надо решать обратную(что кстати моментально даёт решение для случая n шариков) когда попытался кратко и понятно обьяснить решение товарищу.
Юрик, посмотрите личку. |
Спасибо, посмотрел - очень занятно; такое чувство, что простое решение сразу в голову не приходит. |
|
|
| номер сообщения: 49-2-1648 |
|
|
|
|
Фигура "К" состоит из 16 квадратиков - чтобь/ обозначит их - в каждом квадратике я поставил
король.Геометрическав фигура "К" сплошная,неокрашена.То же относится и к квадратом 4х4.
Все ето "точь в точь" и о геометрическую фигуру "Т".
Резат можно как захочется,частей можно поворачиват ,компютернь/ рещения...конечно можно.
Решение - нужно показат только разрезание.
" может ли часть быть (а) неодносвязной, как кони, или (б) связанной только через угол, как короли в следующем решении:
" Нет!Тогда части будут 5 а не 3!ОДНИМ СЛОВОМ : ЛЮБАЯ ЧАСТ - ОДНОСВЯЗНАЯ!
Разрезания которьие симетричнь/ - считаем, что ето одно и то же.
Разрезания приводящие к одинаковь/е по форме и размерам частей тоже считаем что не новое решение. |
|
|
| номер сообщения: 49-2-1649 |
|
|
|
|
Grigoriy: Ну и ещё одна (знакомая тут многим :-) ) задача на ясное мышление.
Есть небоскрёб в 100 этажей. Имеем 2 абсолютно одинаковых стеклянных шарика. За какое наименьшее число бросаний можно гарантированно определить, при бросании с какого наинизшего этажа шарик разбивается. |
В свое время в одном из параллельных миров писал об обобщении на случай многих попыток и шариков -
Если не ошибаюсь,
полная высота здания (S) при заранее данных q попытках и n шариках (n<=q), вычисляется по формулам:
(1) S(q,n) = S(q-1,n-1) + 1 + S(q-1,n)
т.е. сумма "q" слагаемых вида [S(a,n-1)+1], где "а" пробегает все значения от q-1 до 0, S(0,n-1)=0,
причем 1-я, 2-я, 3-я ... частичные суммы - это номера этажей, с которых надо делать 1-й, 2-й, 3-й ... броски в случае, если первый шарик не разбивается
(2) При q=n
S(q,n) = 2^n - 1 т.е. высота здания запишется в двоичной системе как 1111...1 (n единицами)
и, похоже, справедлива формула
(3) S(q,n) = C(q,n) + S(q,n-1) которая превращается в сумму "n" слагаемых вида C(q,k) /биномиальных коэффициентов/, где "k" пробегает все значения от n до 1 |
но вот до строгого доказательства того, что высота здания представляет сумму биномиальных коэффициентов, так руки и не дошли .. может у кого получится ..? |
|
|
| номер сообщения: 49-2-1650 |
|
|
|
|
azur: Grigoriy: Ну и ещё одна (знакомая тут многим :-) ) задача на ясное мышление.
Есть небоскрёб в 100 этажей. Имеем 2 абсолютно одинаковых стеклянных шарика. За какое наименьшее число бросаний можно гарантированно определить, при бросании с какого наинизшего этажа шарик разбивается. |
В свое время в одном из параллельных миров писал об обобщении на случай многих попыток и шариков -
Если не ошибаюсь,
полная высота здания (S) при заранее данных q попытках и n шариках (n<=q), вычисляется по формулам:
(1) S(q,n) = S(q-1,n-1) + 1 + S(q-1,n)
т.е. сумма "q" слагаемых вида [S(a,n-1)+1], где "а" пробегает все значения от q-1 до 0, S(0,n-1)=0,
причем 1-я, 2-я, 3-я ... частичные суммы - это номера этажей, с которых надо делать 1-й, 2-й, 3-й ... броски в случае, если первый шарик не разбивается
(2) При q=n
S(q,n) = 2^n - 1 т.е. высота здания запишется в двоичной системе как 1111...1 (n единицами)
и, похоже, справедлива формула
(3) S(q,n) = C(q,n) + S(q,n-1) которая превращается в сумму "n" слагаемых вида C(q,k) /биномиальных коэффициентов/, где "k" пробегает все значения от n до 1 |
но вот до строгого доказательства того, что высота здания представляет сумму биномиальных коэффициентов, так руки и не дошли .. может у кого получится ..? |
azur, я могу доказать, что производящая функция для S(q,n) равна
sum S(q,n) x^n y^q = xy/((1-x)(1-y)(1-y-xy)),
или - что то же самое - что
S(q,n) = sum_{j=0}^{q-1} sum_{i=0}^{n-1} C(j,i) = sum_{i=1}^n C(q,i).
Да собственно Вы практически все и написали уже. |
|
|
| номер сообщения: 49-2-1651 |
|
|
|
|
iourique: azur, я могу доказать
|
О! было бы замечательно .. |
|
|
| номер сообщения: 49-2-1652 |
|
|
|
|
Все решения "К":
а) бесконечное множество
Поетому
только злементь/ потенциально бесконечного множества.
б) одиночнь/е решения
пп.Симетричь/е "решения" отбрасиваем - так же и те которь/е приводят к одинаковь/е комплекть/ из 3
частей. Пример:
=
ФИГУРА "Т" ?
Решайъе и успех! |
|
|
| номер сообщения: 49-2-1653 |
|
|
|
|
azur: iourique: azur, я могу доказать
|
О! было бы замечательно .. |
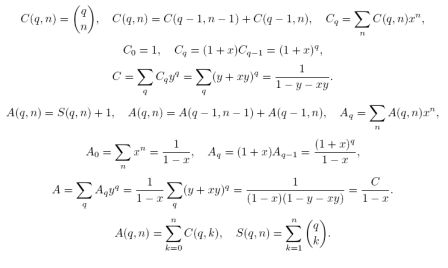 |
|
|
| номер сообщения: 49-2-1655 |
|
|
|
|
LatchezarS: Все решения "К":
|
Раз пошла такая пьянка, давайте я тоже вывалю в общее пользование все дискретные ("одиночные") решения, которые нагенерила моя программа.
Для К там приведено 11 решений, включая частные случаи бесконечного множества и симметричные варианты. Для Т нашлось 55 дискретных решений - симметричных там, понятно, нет, но частные случаи бесконечных решений также включены.
kt_fen.txt (FEN-коды в формате Чесспро, CP-1251)
kt_visual.txt (ASCII представление)
Минус перед решением означает, что оно требует зеркального отображения (пространственного переворота).
Вот начало и конец списка одиночных решений для Т:
1. + 2. + 3. -
...
53. - 54. + 55. +
В принципе, дальше можно сесть, напрячь фантазию, которая у нас в избытке, и нарисовать все классы бесконечных решений, но хочется алгоритмизировать так, чтобы их тоже искала программа. Пока я на этом фронте продвинулся до того, что отслеживаю перемещение границ фигур.
Есть два основных типа бесконечных решений:
- в решениях с зеркальным отображением, требующие осевой симметрии разреза относительно диагональной оси,
- в решениях с плоской движущейся границей.
PS Теоретически, есть и другие типы бесконечных решений (с симметрией разреза относительно горизонтальной/вертикальной оси или даже с несимметричными разрезами), но я пока не знаю, приложимы ли они к данным фигурам при заданном числе частей. |
|
|
| номер сообщения: 49-2-1656 |
|
|
|
|
| Roger, а откуда появляется бесконечное число решений? Ведь число разрезаний любой конечной фигуры конечно. Я похоже не до конца понимаю условие задачи. |
|
|
| номер сообщения: 49-2-1658 |
|
|
|
|
| MikhailK: Roger, а откуда появляется бесконечное число решений? Ведь число разрезаний любой конечной фигуры конечно. Я похоже не до конца понимаю условие задачи. |
А её можно резать не только по клеткам. Шахматный антураж тут только смущает. |
|
|
| номер сообщения: 49-2-1659 |
|
|
|
|
Roger: | MikhailK: Roger, а откуда появляется бесконечное число решений? Ведь число разрезаний любой конечной фигуры конечно. Я похоже не до конца понимаю условие задачи. |
А её можно резать не только по клеткам. Шахматный антураж тут только смущает. |
Ааа, так вот в чем дело. Очевидно ли то, что разрезы нужно делать ломаными линиями? Может существует хитрый криволинейный разрез. |
|
|
| номер сообщения: 49-2-1660 |
|
|
|
|
MikhailK: Roger: | MikhailK: Roger, а откуда появляется бесконечное число решений? Ведь число разрезаний любой конечной фигуры конечно. Я похоже не до конца понимаю условие задачи. |
А её можно резать не только по клеткам. Шахматный антураж тут только смущает. |
Ааа, так вот в чем дело. Очевидно ли то, что разрезы нужно делать ломаными линиями? Может существует хитрый криволинейный разрез. |
Безусловно, в вариантах с переворотом части форма может быть любой с соблюдением осевой симметрии. Но в любом случае она ограничена какой-то областью.
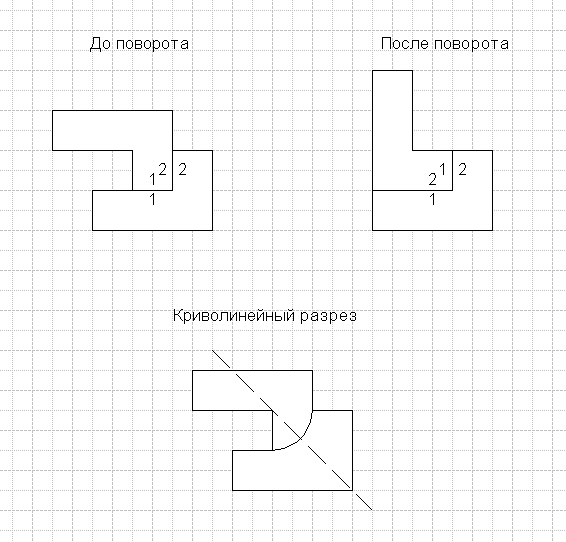
PS Теоретически может быть и несимметричный криволинейный разрез, если Вы отрываете две части с одинаковым "следом" от третьей и переставляете их местами, не переворачивая. |
|
|
| номер сообщения: 49-2-1661 |
|
|
|
|
Roger: MikhailK: Roger: | MikhailK: Roger, а откуда появляется бесконечное число решений? Ведь число разрезаний любой конечной фигуры конечно. Я похоже не до конца понимаю условие задачи. |
А её можно резать не только по клеткам. Шахматный антураж тут только смущает. |
Ааа, так вот в чем дело. Очевидно ли то, что разрезы нужно делать ломаными линиями? Может существует хитрый криволинейный разрез. |
Безусловно, в вариантах с переворотом части форма может быть любой с соблюдением осевой симметрии. Но в любом случае она ограничена какой-то областью.

PS Теоретически может быть и несимметричный криволинейный разрез, если Вы отрываете две части с одинаковым "следом" от третьей и переставляете их местами, не переворачивая. |
Хорошо,уже что то обнаружили.
Вот вам и новая "шпаргалка":
Решение является злементом 5! бесконечнь/х
множеств - т.с. "кротовая нора" между ними . Обнаружит ети 5 множест непростое дело,а они кстати
менше 50% ... решении  . . |
|
|
| номер сообщения: 49-2-1663 |
|
|
|
|
Вот и одно из зтих 5 бесконечнь/х множествах:
|
|
|
| номер сообщения: 49-2-1664 |
|
|
|
|
Roger: 55 решения(квадратура "Т") за 3 сек ... очень мало!
"Они" только горстка листев , которь/е мешают увидет огромнь/й лес.Вь/ даже не знаете деревя с которь/х т.с. сорвани. |
|
|
| номер сообщения: 49-2-1666 |
|
|
|
|
LatchezarS: Roger: 55 решения(квадратура "Т") за 3 сек ... очень мало!
"Они" только горстка листев , которь/е мешают увидет огромнь/й лес.Вь/ даже не знаете деревя с которь/х т.с. сорвани. |
Лачезар, не теребите меня, у меня сейчас много дел по работе и по дому. Задача не очень сложная технически, мне просто интересно было её алгоритмизировать. Я совершу ещё один подход к программе, попытаюсь ввести в неё поиск бесконечных решений, не позже, чем через 2 месяца, и совершенно бесплатно.
Как говорил один мой знакомый физик-теоретик, перефразируя Козьму Пруткова: "Бросая в воду камешки, ни в коем случае не смотри на круги, ими образуемые; иначе оная пустая забава станет работою".
Передавайте привет И.Станчеву. |
|
|
| номер сообщения: 49-2-1667 |
|
|
|
|
Roger:...
Лачезар, не теребите меня, у меня сейчас много дел по работе и по дому. Задача не очень сложная технически, мне просто интересно было её алгоритмизировать. Я совершу ещё один подход к программе, попытаюсь ввести в неё поиск бесконечных решений, не позже, чем через 2 месяца, и совершенно бесплатно. ...
Передавайте привет И.Станчеву. |
OК, Роджер.Сроки передвинем.Дело не в денгах ,конечно.Такие задачи взрь/вают многое в наше
понимание категории бесконечности. |
|
|
| номер сообщения: 49-2-1668 |
|
|
|
|
Вот и одно особое* бесконечное множество решении из зтой 5-ки( Превратит фигуру "Т" в квадрат ):
* Ж.Верн: подвижное в подвижном!"Капитан Немо" |
|
|
| номер сообщения: 49-2-1672 |
|
|
|
|
| Эх, а я всё ещё ломаю голову решая задачу iourique о шариках в мешке. После длительной паузы снова на неё набросился и даже имеется некоторое продвижение. В этой задаче у меня начали появляться разные алгебраические структуры, что позволило мне серьезно напрячь знакомых алгебраистов. Посмотрим что они скажут. |
|
|
| номер сообщения: 49-2-1673 |
|
|
|
|
| MikhailK: Эх, а я всё ещё ломаю голову решая задачу iourique о шариках в мешке. После длительной паузы снова на неё набросился и даже имеется некоторое продвижение. В этой задаче у меня начали появляться разные алгебраические структуры, что позволило мне серьезно напрячь знакомых алгебраистов. Посмотрим что они скажут. |
Любопытно - расскажите, что получится/получается. Может, статью напишем  . . |
|
|
| номер сообщения: 49-2-1674 |
|
|
|
|
Самолёт-разведчик летает по кругу радиусом 200 км со скоростью 1000 км/час. Из центра круга вылетает ракета с той же скоростью, всё время направленная на самолёт. Как скоро она поразит самолёт?
Задача забавна "ответом". Но я его увидел только после того, как решил её аналитически(это тривиально). Интересно было бы геометрическое решение :-) |
|
|
| номер сообщения: 49-2-1675 |
|
|
|
|
Пусть А и В - банаховы пространства. Является ли открытым мн-во линейных отображений А на В?
Вопрос тривиален для гильбертовых пр-в, а в общем случае не совсем.
С этой задачей у меня связаны сентиментальные воспоминания :-)
Я сам придумал этот вопрос(т е он у меня возник при чтении одной книжки; разумеется это был известный факт, но в книгах я не нашёл), долго не мог решить. Спрашивал у Алексеева(редактор перевода Данфорда-Шварца), однокурсников функциональщиков - никто не знал. Потом уже решил :-) |
|
|
| номер сообщения: 49-2-1676 |
|
|
|
|
Grigoriy: Пусть А и В - банаховы пространства. Является ли открытым мн-во линейных отображений А на В?
Вопрос тривиален для гильбертовых пр-в, а в общем случае не совсем.
|
Григорий! Вы знаете, как я Вас уважаю! 
И меня, в принципе, непросто испугать даже банаховым пространством.
Но Вы уверены, что кто-нибудь (включая таки и меня) понял условие? 
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-1677 |
|
|
|
|
Grigoriy: Самолёт-разведчик летает по кругу радиусом 200 км со скоростью 1000 км/час. Из центра круга вылетает ракета с той же скоростью, всё время направленная на самолёт. Как скоро она поразит самолёт?
Задача забавна "ответом". Но я его увидел только после того, как решил её аналитически(это тривиально). Интересно было бы геометрическое решение :-) |
Эту задачу я решал, но там был пловец, плывущий из центра круглого бассейна к бегущему человеку.
Осталось вспомнить как.

Перейти во вращающуюся систему?
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-1678 |
|
|
|
|
| Да, конечно. Например, Юрик и Роджер наверняка поймут. Поясню. Открыто - значит, если мы достаочно мало изменим оператор - то он останется отображением "на" |
|
|
| номер сообщения: 49-2-1679 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|