|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
ygeshelin:
| iourique: Похоже, как это ни смешно, что последовательность немонотонна. |
Будем рассуждать методом от противного. Допустим, что она не монотонна. Тогда получается, что при добавлении n+1 й окружности отношение r / R1 стало меньше, чем на предыдущем этапе. r у нас не меняется. Значит, R1 стало больше. Такого не может быть. Ведь R1, как и каждая другая внешная окружность, должно уменьшиться - иначе не втиснуть ещё одну. Значит, исходное предположение неверно. |
Это не совсем так.
Представьте себе картинку с 28 окружностями, касающимися друг друга по кругу. Теперь попытаемся вписать туда 29-ую окружность радиуса r phi^29, касающуюся 28-ой и центральной окружностей. Есть 3 варианта: она пересечет первую окружность, коснется ее, или не достанет до нее вовсе. Судя по всему, реализуется последний вариант. При этом единственный способ замкнуть цепочку - это увеличить phi. Тогда 28-ая окружность будет пересекать первую, а 29-ая - касаться первой и 28-ой. |
|
|
| номер сообщения: 49-2-11244 |
|
|
|
|
| ygeshelin: Док-во по методу мат индукции здесь возможно... Всё это применимо в данном случае, можно доказать, что каждое последующее увеличение FI становится меньше. Впрочем, крутые математики не считают этот метод абсолютно строгим |
кстати да, уменьшение увеличения подвержено (в принципе) доказательству методом мат. индукции, но нас колышет бОльше: доказать убывание к нулю увеличения, как раз это мерещится неподвластным методу 
| ygeshelin: крутые математики не считают этот метод абсолютно строгим |

вроде сам не слабак и метод мне не претит 
| ygeshelin: чтобы найти значение предела, тут нужно в бесконечный ряд Тейлора разложить и вычислить сумму. Это у меня пока не получилось |
какую сумму, причём тут ряд Тейлора, какую функцию будет разлагать?  |
|
|
| номер сообщения: 49-2-11245 |
|
|
|
|
| Вы, Хайдук, не просто чайник, Вы какой-то бездонный чайник; агрегат по производству пара в неограниченных количествах. |
|
|
| номер сообщения: 49-2-11246 |
|
|
|
|

примерчики с паром в студию, плиз  |
|
|
| номер сообщения: 49-2-11247 |
|
|
|
|
Хайдук: 
примерчики с паром в студию, плиз  |
Вот. |
|
|
| номер сообщения: 49-2-11248 |
|
|
|
|
желательно поконкретнее, поскольку ссылка видимо не пляшет на пользу ожидаемому предназначению 
ЗЫ. от знатока как вас, юрик, ожидал критики моих потуг по части текущей задачки, АТО со своей стороны внимательно слежу за вашими и воздерживаюсь от опрометчивых выпадов если не заметили  |
|
|
| номер сообщения: 49-2-11249 |
|
|
|
|
iourique: ygeshelin:
| iourique: Похоже, как это ни смешно, что последовательность немонотонна. |
Будем рассуждать методом от противного. Допустим, что она не монотонна. Тогда получается, что при добавлении n+1 й окружности отношение r / R1 стало меньше, чем на предыдущем этапе. r у нас не меняется. Значит, R1 стало больше. Такого не может быть. Ведь R1, как и каждая другая внешная окружность, должно уменьшиться - иначе не втиснуть ещё одну. Значит, исходное предположение неверно. |
Это не совсем так.
Представьте себе картинку с 28 окружностями, касающимися друг друга по кругу. Теперь попытаемся вписать туда 29-ую окружность радиуса r phi^29, касающуюся 28-ой и центральной окружностей. Есть 3 варианта: она пересечет первую окружность, коснется ее, или не достанет до нее вовсе. Судя по всему, реализуется последний вариант. При этом единственный способ замкнуть цепочку - это увеличить phi. Тогда 28-ая окружность будет пересекать первую, а 29-ая - касаться первой и 28-ой. |
Другими словами, 28 - максимальная длина цепочки, в которой окружности не пересекаются. Или, еще по-другому, phi = 1.2151325464653 - максимальное значение, при котором цепочка замыкается. |
|
|
| номер сообщения: 49-2-11250 |
|
|
|
|
iourique:
Это не совсем так.
Представьте себе картинку с 28 окружностями, касающимися друг друга по кругу. Теперь попытаемся вписать туда 29-ую окружность радиуса r phi^29, касающуюся 28-ой и центральной окружностей. Есть 3 варианта: она пересечет первую окружность, коснется ее, или не достанет до нее вовсе. Судя по всему, реализуется последний вариант. При этом единственный способ замкнуть цепочку - это увеличить phi. Тогда 28-ая окружность будет пересекать первую, а 29-ая - касаться первой и 28-ой. |
Не совсем понял рассуждение: что значит - попытаемся вписать? По условию задачи 29-ю окружность радиуса r * phi^29 надо вписать так, чтобы она касалась не только 28-ой и центральной окружностей, но также и первой. Для этого надо освободить для неё место, а значит, уменьшить каждый из 28 радиусов, в том числе R1. У нас R1 = r * phi. Значит, phi станет меньше, а PSI - больше, т.е. поднимется до ассимптоты. |
|
|
| номер сообщения: 49-2-11251 |
|
|
|
|
Хайдук:
какую сумму, причём тут ряд Тейлора, какую функцию будет разлагать?  |
Например, формулу, запощенную iourique 06.01.2016 | 02:19:06. Или через арккосинус. |
|
|
| номер сообщения: 49-2-11252 |
|
|
|
|
ygeshelin: iourique:
Это не совсем так.
Представьте себе картинку с 28 окружностями, касающимися друг друга по кругу. Теперь попытаемся вписать туда 29-ую окружность радиуса r phi^29, касающуюся 28-ой и центральной окружностей. Есть 3 варианта: она пересечет первую окружность, коснется ее, или не достанет до нее вовсе. Судя по всему, реализуется последний вариант. При этом единственный способ замкнуть цепочку - это увеличить phi. Тогда 28-ая окружность будет пересекать первую, а 29-ая - касаться первой и 28-ой. |
Не совсем понял рассуждение: что значит - попытаемся вписать? По условию задачи 29-ю окружность радиуса r * phi^29 надо вписать так, чтобы она касалась не только 28-ой и центральной окружностей, но также и первой. Для этого надо освободить для неё место, а значит, уменьшить каждый из 28 радиусов, в том числе R1. У нас R1 = r * phi. Значит, phi станет меньше, а PSI - больше, т.е. поднимется до ассимптоты. |
Я должен был сказать "впишем". Я вписываю 29-ую окружность не согласно условию, а как сказано выше - для иллюстрации. |
|
|
| номер сообщения: 49-2-11253 |
|
|
|
|
| iourique: 28 - максимальная длина цепочки, в которой окружности не пересекаются. Или, еще по-другому, phi = 1.2151325464653 - максимальное значение, при котором цепочка замыкается. |
| ygeshelin: По условию задачи 29-ю окружность радиуса r * phi^29 надо вписать так, чтобы она касалась не только 28-ой и центральной окружностей, но также и первой. Для этого надо освободить для неё место, а значит, уменьшить каждый из 28 радиусов, в том числе R1. У нас R1 = r * phi. Значит, phi станет меньше, а PSI - больше, т.е. поднимется до ассимптоты. |
за исключением недоказанной ассимптоты прокола у почтённого ygeshelin-а пока не застукиваю...  |
|
|
| номер сообщения: 49-2-11254 |
|
|
|
|
| ygeshelin: формулу, запощенную iourique 06.01.2016 | 02:19:06. Или через арккосинус. |
iourique: У меня получается не совсем так. Мы ищем решение уравнения
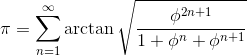
Численно у меня выходит что-то около 0.823928674, что близко к корню из пяти на е, но ему не равно. |
это уравнение/равенство, а не функция, ygeshelin, не вижу как ряд Тейлора поможет найти его корень, если таковому быть  |
|
|
| номер сообщения: 49-2-11255 |
|
|
|
|
| iourique: Я должен был сказать "впишем". |
Но я не вижу, как это меняет дело.
| iourique:Я вписываю 29-ую окружность не согласно условию, а как сказано выше - для иллюстрации. |
Но ведь всё равно делать это надо, не нарушая условие задачи. |
|
|
| номер сообщения: 49-2-11256 |
|
|
|
|
Хайдук:
за исключением недоказанной ассимптоты прокола у почтённого ygeshelin-а пока не застукиваю...  |
Думаю, что наличие ассимптоты доказано. Неизвестно лишь её значение, интуиция может и подвести.
Хайдук:
это уравнение/равенство, а не функция,
|
В этом уравнении под знаком суммы - функция, о ней и речь.
Хайдук:
не вижу как ряд Тейлора поможет найти его корень, если таковому быть
|
Если окажется, что при каждом n ряд сходимый (должно быть так), то попытаться в его разложение подставить е/sqrt(5) и найти его сумму.
Это может удаться, а может и нет из-за трансцендентности. Если окажется, что сумма сумм равна pi (или в случае арккосинуса - 2pi), всё станет на свои места.
Если нет, то не знаю, не будем гадать на кофейной гуще. |
|
|
| номер сообщения: 49-2-11257 |
|
|
|
|
| iourique: Другими словами, 28 - максимальная длина цепочки, в которой окружности не пересекаются. Или, еще по-другому, phi = 1.2151325464653 - максимальное значение, при котором цепочка замыкается. |
Виноват, как-то пропустил эти Ваши слова, или Вы потом добавили. Вы хотите сказать, что начиная с n = 29 уравнение не имеет рациональных корней? Думаю, что такого не может быть, и вот почему. Всегда можно подобрать настолько малое PHI, что последняя окружность не достанет до первой. И всегда можно подобрать настолько большое PHI, что они пересекутся. Корень обязательно будет посередине, собственно, алгоритм так его и ищет, максимально сужая интервал. И ведь находит. |
|
|
| номер сообщения: 49-2-11258 |
|
|
|
|
ygeshelin: | iourique: Другими словами, 28 - максимальная длина цепочки, в которой окружности не пересекаются. Или, еще по-другому, \phi = 1.2151325464653 - максимальное значение, при котором цепочка замыкается. |
Виноват, как-то пропустил эти Ваши слова, или Вы потом добавили. Вы хотите сказать, что начиная с n = 29 уравнение не имеет рациональных корней? Думаю, что такого не может быть, и вот почему. Всегда можно подобрать настолько малое PHI, что последняя окружность не достанет до первой. И всегда можно подобрать настолько большое PHI, что они пересекутся. Корень обязательно будет посередине, собственно, алгоритм так его и ищет, максимально сужая интервал. И ведь находит. |
Давайте я еще раз попробую объяснить:
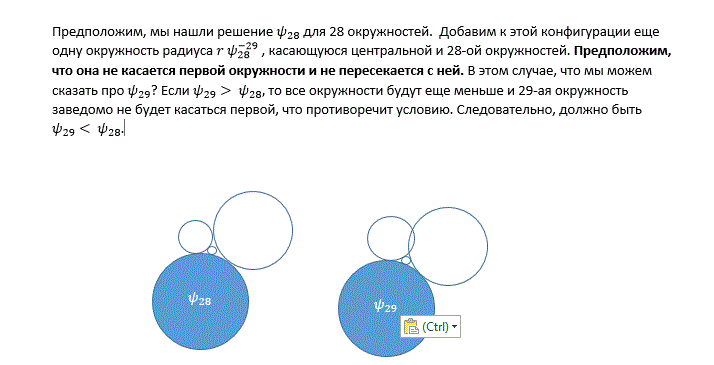 |
|
|
| номер сообщения: 49-2-11259 |
|
|
|
|
iourique: ygeshelin: | iourique: Другими словами, 28 - максимальная длина цепочки, в которой окружности не пересекаются. Или, еще по-другому, \phi = 1.2151325464653 - максимальное значение, при котором цепочка замыкается. |
Виноват, как-то пропустил эти Ваши слова, или Вы потом добавили. Вы хотите сказать, что начиная с n = 29 уравнение не имеет рациональных корней? Думаю, что такого не может быть, и вот почему. Всегда можно подобрать настолько малое PHI, что последняя окружность не достанет до первой. И всегда можно подобрать настолько большое PHI, что они пересекутся. Корень обязательно будет посередине, собственно, алгоритм так его и ищет, максимально сужая интервал. И ведь находит. |
Давайте я еще раз попробую объяснить:
 |
Теперь понял. На первый взгляд всё логично. Но давайте я Вам приведу симметричное рассуждение. Итак, по-Вашему выходит, что PSI_29 меньше, чем правильно найденное PSI_28. Давайте возьмём вот это PSI_29 и по нему рассчитаем радиусы для конфигурации из 28 окружностей. Что получится? Эти 28 окружностей станут больше, чем рассчитанные по правильно найденному PSI_28. И последняя окружность пересечёт первую, что противоречит условию задачи. А теперь добавим 29-ю окружность, рассчитав её радиус по этому же значению PSI_29. Она-то уж тем более пересечётся с первой! Поэтому мне кажется, что Ваш сценарий невозможен. То есть, возвращаясь к Вашей фразе, которую Вы выделили жирным шрифтом:
Предположим, что она не касается первой окружности и не пересекается с ней.
Выходит, что это предположение неверно, такого не может быть. Если я Вас правильно понял.
Это также можно проверить программным путём, добавляя на каждом цикле лишнюю окружность и проверяя, пересекается ли она с первой. |
|
|
| номер сообщения: 49-2-11260 |
|
|
|
|
| Юрик обычно бывает прав, и тут, кажется, тоже. |
|
|
| номер сообщения: 49-2-11261 |
|
|
|
|
угу, казалось, что всегда (для любого n) можно найти точно (с касанием) замыкающуюся цепочку кругов фиксированного psi; стоит задуматься, однако, и приходишь к выводу, что это скорее сильное и никак НЕ обязательное для любого числа окружающих кругов предположение: дабы выполнялось, дополнительный круг со старым psi должен всегда пересекать первый круг, тем самым обеспечивая ресурс для уменьшения всех кругов, что в действительности никак не "естественно" и (как оказалось) не обязательно 
не знаю заметил ли юрик, но по совокупности бреда про пределы, метод мат. индукции, ряд Тейлора и пр. я сразу почуял, что нашему новому коллеге ygeshelin не хватает того, что обзывают математической культурой - а dirty практик, привыкший шлепать компом с серпом, молотом и ... матерью. Можешь впасть в заблуждение до поры до времени, но фундаментального понимания не пропёшь  |
|
|
| номер сообщения: 49-2-11262 |
|
|
|
|
| ygeshelin: Давайте возьмём вот это PSI_29 и по нему рассчитаем радиусы для конфигурации из 28 окружностей. Что получится? Эти 28 окружностей станут больше, чем рассчитанные по правильно найденному PSI_28. И последняя окружность пересечёт первую, что противоречит условию задачи. А теперь добавим 29-ю окружность, рассчитав её радиус по этому же значению PSI_29. Она-то уж тем более пересечётся с первой! |
Последняя фраза не верна. Представьте, что мы построили некоторую касательную спираль cнаружи к нашей серии окружностей. При уменьшении радиуса угол, под которым она сечёт радиус-векторы из центра нулевой окружности, стремится к константе, π/2 - 2*arcsin((ψ - 1)*(ψ + 1))
В то же время, с увеличением N хвост этой спирали пытается залезть во всё более узкую щель между первой и нулевой окружностью в точке, где касательная к первой окружности будет пересекаться с радиус-вектором из центра нулевой окружности под углом π/2 - arccos((1 + 1/ψ + 1/ψ^N - 1/ψ^(N-1))/(1 + 1/ψ + 1/ψ^N + 1/ψ^(N-1))) - arccos((1 + 1/ψ + 1/ψ^N - 1/ψ^(N+1))/(1 + 1/ψ + 1/ψ^N + 1/ψ^(N+1))).
У меня получилось, что при постоянном ψ=1.215 эти два угла равны при N=28. То есть я зафиксировал ψ и решил уравнение относительно N, получив 28 с точностью до четвёртого знака, что, видимо, отражает тот факт, что значение 1.215 я не высосал из пальца, а взял из юриковых экзерсисов.
 |
|
|
| номер сообщения: 49-2-11263 |
|
|
|
|
Roger:
| ygeshelin: Давайте возьмём вот это PSI_29 и по нему рассчитаем радиусы для конфигурации из 28 окружностей. Что получится? Эти 28 окружностей станут больше, чем рассчитанные по правильно найденному PSI_28. И последняя окружность пересечёт первую, что противоречит условию задачи. А теперь добавим 29-ю окружность, рассчитав её радиус по этому же значению PSI_29. Она-то уж тем более пересечётся с первой! |
Последняя фраза не верна. |
Странно: последняя фраза, по-моему, с очевидностью вытекает из предыдущих. Если уже 28-я окружность не помещается на кольце, то 29-я и подавно. Может быть, Вы укажете на более раннюю ошибку в моём рассуждении? Попробую ещё раз его изложить, может, я это плохо сделал. Вернёмся к предположению iourique:
iourique:
Предположим, мы нашли решение PSI_28 для 28 окружностей. Добавим к этой конфигурации ешё одну окружность радиуса r * PSI_28 ^-29, касающуюся центральной и 28-ой окружностей. Предположим, что она не касается первой окружности и не пересекается с ней. |
В фразе, которую iourique выделил жирным шрифтом, ключевое слово - предположим. Итак, предположим, что такое вдруг впервые случилось при n = 28, и посмотрим, к чему это предположение приведёт. В этом случае, как убедительно показал iourique, окажется, что PSI_29 < PSI_28, где PSI_29 - решение для 29 окружностей. Хорошо, пойдём дальше. Попробуем выстроить цепочку из 29 окружностей, радиусы которых рассчитаны по этому PSI_29. И вот тут оказывается, что уже 28-я из этих 29 пересекается с 1-й. Потому что все радиусы больше рассчитанных по PSI_28. Значит, 29-я, тем более, пересечётся с первой, причём бОльшая часть 29-й окажется внутри 1-й. Условие задачи будет нарушено. А это означает, что PSI_29 - не есть решение нашего уравнения. Мы пришли к логическому противоречию, значит, исходное предположение iourique неверно. Стало быть, остаётся в силе моё рассуждение, где я показал, что PSI_29 > PSI_28 (пост 08.01.2016 | 00:16:50)
Roger:
Представьте, что мы построили некоторую касательную спираль cнаружи к нашей серии окружностей. При уменьшении радиуса угол, под которым она сечёт радиус-векторы из центра нулевой окружности, стремится к константе, π/2 - 2*arcsin((ψ - 1)*(ψ + 1))
В то же время, с увеличением N хвост этой спирали пытается залезть во всё более узкую щель между первой и нулевой окружностью в точке, где касательная к первой окружности будет пересекаться с радиус-вектором из центра нулевой окружности под углом π/2 - arccos((1 + 1/ψ + 1/ψ^N - 1/ψ^(N-1))/(1 + 1/ψ + 1/ψ^N + 1/ψ^(N-1))) - arccos((1 + 1/ψ + 1/ψ^N - 1/ψ^(N+1))/(1 + 1/ψ + 1/ψ^N + 1/ψ^(N+1))).
У меня получилось, что при постоянном ψ=1.215 эти два угла равны при N=28. То есть я зафиксировал ψ и решил уравнение относительно N, получив 28 с точностью до четвёртого знака, что, видимо, отражает тот факт, что значение 1.215 я не высосал из пальца, а взял из юриковых экзерсисов.
 |
Я не разобрался в Ваших формулах, т.е. не могу сказать, что понимаю, как они выведены, верю Вам на слово, конечно. У Вас получилось, что если задаться приблизительным значением psi = 1.215, то равенство обозначенных Вами углов достигается при n = 28. И что Вы хотите этим сказать, что отсюда следует? Заметьте, что psi = 1.215 с точностью до 3-го знака не только при n = 28, но и при любом n от 23 до 34 (см., например, пост iourique от 07.01.2016 | 18:12:05; его значения совпадают с моими, см. мой пост 07.01.2016 | 06:56:21). Не исключено, что если Вы возьмёте psi = 1.214 или psi = 1.218, у Вас приблизительно тоже получится n = 28. Какое всё это имеет отношение к делу? |
|
|
| номер сообщения: 49-2-11264 |
|
|
|
|
Роджер рулит!   |
|
|
| номер сообщения: 49-2-11266 |
|
|
|
|
| ygeshelin: А теперь добавим 29-ю окружность, рассчитав её радиус по этому же значению PSI_29. Она-то уж тем более пересечётся с первой! |
Я даже ведь картинку нарисовал(справа), где показано, как 28-ая окружность с первой пересекается, а 29-ая - касается и 28-ой и первой. |
|
|
| номер сообщения: 49-2-11267 |
|
|
|
|
iourique: | ygeshelin: А теперь добавим 29-ю окружность, рассчитав её радиус по этому же значению PSI_29. Она-то уж тем более пересечётся с первой! |
Я даже ведь картинку нарисовал(справа), где показано, как 28-ая окружность с первой пересекается, а 29-ая - касается и 28-ой и первой. |
Вот оно что! Я на эту картинку смотрел, но не так её понимал. Признаю, что я был неправ, когда говорил о логическом противоречии. Нет его у Вас. Да, это тот случай, когда что-то кажется очевидным, а потом - БАЦ, и видишь, что ты неправ.
Но хотя и нет у Вас логического противоречия, надо бы проверить, действительно ли так дело обстоит с Вашим предположением. Навскидку странно как-то получается, что начиная с n = 29 каждая последняя окружность вот так точно укладывается в треугольник из дуг. Возможно, Roger мне это доказывал, но я не понял его рассуждение. Подумаю ещё над ним. Спасибо всем.
И наконец, даже если psi начинает уменьшаться, начиная с n = 29, то без конца это уменьшение происходить не может. Например, очевидно, что оно не может стать меньше 1. (Ещё одна очевидная очевидность  ?) Нет, если Вы правы, то что-то интересное должно произойти с функцией дальше. Кстати, Вы рассчитывали fi = 1/psi для n = 200, и оно мало отличалось от случая n = 34. Что же происходит в промежутке n = [35 - 200]? Неужели функция плавно изменяется на такую малую величину? Или она осцилирует, что говорит в пользу моей теории об ошибках округления? ?) Нет, если Вы правы, то что-то интересное должно произойти с функцией дальше. Кстати, Вы рассчитывали fi = 1/psi для n = 200, и оно мало отличалось от случая n = 34. Что же происходит в промежутке n = [35 - 200]? Неужели функция плавно изменяется на такую малую величину? Или она осцилирует, что говорит в пользу моей теории об ошибках округления? |
|
|
| номер сообщения: 49-2-11268 |
|
|
|
|
| ygeshelin: Что же происходит в промежутке n = [35 - 200]? Неужели функция плавно изменяется на такую малую величину? |
Скорее всего, да, тихонько стремится к пределу в районе 1.2137, но не снизу, как мы предполагали, а сверху.
| Или она осцилирует, что говорит в пользу моей теории об ошибках округления? |
Мне кажется, что осциллировать она не будет, но доказать я это не возьмусь. Численно видно строгое убывание после 28:
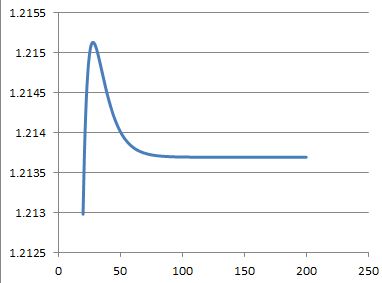 |
|
|
| номер сообщения: 49-2-11269 |
|
|
|
|
| ygeshelin: Не исключено, что если Вы возьмёте psi = 1.214 или psi = 1.218, у Вас приблизительно тоже получится n = 28. Какое всё это имеет отношение к делу? |
Приблизительно получится, да. Например, psi = 1.2136 даёт N = 28.22
| ygeshelin: Я не разобрался в Ваших формулах, т.е. не могу сказать, что понимаю, как они выведены, верю Вам на слово, конечно. |
Первый записанный угол - вот этот
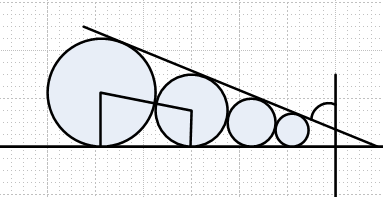
(Картинки для простоты развернуты из полярной системы координат, то есть по X у нас угол, а по Y - радиус). Верхняя касательная, на самом деле - спираль Архимеда. Угол легко посчитать из нарисованной прямоугольной трапеции. Он зависит только от ψ и равен
π/2 - 2*arcsin((ψ - 1)*(ψ + 1))
Второй угол - наклон касательной к последней окружности.
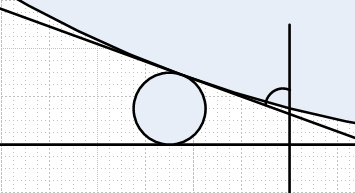
Этот угол зависит как от ψ, так и от N, и равен (из теоремы косинусов)
π/2 - arccos((1 + 1/ψ + 1/ψ^N - 1/ψ^(N-1))/(1 + 1/ψ + 1/ψ^N + 1/ψ^(N-1))) - arccos((1 + 1/ψ + 1/ψ^N - 1/ψ^(N+1))/(1 + 1/ψ + 1/ψ^N + 1/ψ^(N+1)))
Эти два угла примерно равны при N = 28
Если взять ψ(28), и добавить 29-ую окружность, она не пересечётся с первой окружностью (как и все последующие). Для того, чтобы она коснулась, она должна быть немного больше (и дальше), то есть ψ(29) должно быть меньше ψ(28). При этом 28-ая окружность будет пересекаться с первой. То же самое будет и с последующими. |
|
|
| номер сообщения: 49-2-11270 |
|
|
|
|
| Спасибо, iourique и Roger, за подробные разъяснения. |
|
|
| номер сообщения: 49-2-11271 |
|
|
|
|
| ygeshelin: Что же происходит в промежутке n = [35 - 200]? Неужели функция плавно изменяется на такую малую величину? |
| iourique: Скорее всего, да, тихонько стремится к пределу в районе 1.2137, но не снизу, как мы предполагали, а сверху. |
| Или она осцилирует, что говорит в пользу моей теории об ошибках округления? |
iourique: Мне кажется, что осциллировать она не будет, но доказать я это не возьмусь. Численно видно строгое убывание после 28:
 |
смотрю на график и недоумеваю как почтённому ygeshelin-у пришлось заняться задачкой, откуда взял, какой была мотивация, так сказать (тем более, если большинство венков окружающих кругов наступают друг другу на ногу)?  может схОдится, может не схОдится, благо не может не сходИться, если приспичит - ведь дырок-то у (действительных) чисел и планиметрии нет. Таких задач "з бодуна, где сам чёрт ногу сломит" будет бесчисленно, даже несчётно много, прямь застрелиццо можно может схОдится, может не схОдится, благо не может не сходИться, если приспичит - ведь дырок-то у (действительных) чисел и планиметрии нет. Таких задач "з бодуна, где сам чёрт ногу сломит" будет бесчисленно, даже несчётно много, прямь застрелиццо можно  |
|
|
| номер сообщения: 49-2-11272 |
|
|
|
|
| Roger: Если взять ψ(28), и добавить 29-ую окружность, она не пересечётся с первой окружностью (как и все последующие). Для того, чтобы она коснулась, она должна быть немного больше (и дальше), то есть ψ(29) должно быть меньше ψ(28). При этом 28-ая окружность будет пересекаться с первой. То же самое будет и с последующими. |
можем ли считать доказанным, что после ψ(28) ψ(n) будет монотонно уменьшаться, то бишь размер соприкасающихся кругов R кольца будет расти?  если будет потолок/верхняя граница такому неубывающему размеру, то тогда у нерастущего/монотонного ψ(n) будет дно, то бишь точная/самая большая нижняя граница, которую обзывают пределом при неограничено растущем числе n кругов кольца. Думаю, что додумался до такого кольца-потолка с потолковым размером кругов: это будет кольцо, последний круг которого вписан в первом кругу и касается внутреннего круга радиуса r в той же точке, что и первый круг кольца; безусловно предпоследний круг (по меньшей мере) такого кольца-потолка будет пересекать его первый круг. если будет потолок/верхняя граница такому неубывающему размеру, то тогда у нерастущего/монотонного ψ(n) будет дно, то бишь точная/самая большая нижняя граница, которую обзывают пределом при неограничено растущем числе n кругов кольца. Думаю, что додумался до такого кольца-потолка с потолковым размером кругов: это будет кольцо, последний круг которого вписан в первом кругу и касается внутреннего круга радиуса r в той же точке, что и первый круг кольца; безусловно предпоследний круг (по меньшей мере) такого кольца-потолка будет пересекать его первый круг.
несомненно почтённый Роджер смог бы (я не) посчитать значение-дно ψ (скорее ниже точного днища выше) и соответствующее ему число кругов n с потолковыми радиусами, если я не прокололся, конечно 
ЗЫ. сомневаюсь, что любитель красоты в Лувре и жызни - почтённый ygeshelin - найдёт её в ума холодных потугах сферху  |
|
|
| номер сообщения: 49-2-11294 |
|
|
|
|
| А вот интересно дружите ли вы со сложением чисел. Расшифруйте пример ELZA+ISAAC=LOVERS(Эльза и Исаак-любовники). |
|
|
| номер сообщения: 49-2-11296 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2026 гг. |
|
|
|