|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
rudolf:| На слух и вне контекста это можно принять за глагол |
| Уменьшительное от этого вышло из обихода намного позже. И, к тому же, не безвозвратно |
. в первом случае я не сильно напрягаясь могу найти десяток вариантов, в другом-считаные единицы. роль случая в выборе ответа в первом варианте огромна, во втором-намного меньше.
[..] думаю, что плохи обе крайности |
Во-вот! Наличие столь разных по степени конкретности подсказок и призвано "усреднить" эти крайности 
| Вы абсолютно правы: полностью избежать дуалей в принципе невозможно. |
я удовлетворен ответом  поэтому поэтому |
... поскипали продолжение моей мысли 
| отгадав авторский ответ они абсолютно уверены в его верности. А придумав альтернативный, сомневаются |
это вполне понятно как раз. ответив верно, человек не видит причин искать ему еще дополнительные варианты. зачем? а нашедший сразу другой вариант (тоже верный по условиям подсказок), сомневается как минимум. было бы удивительно , если бы было по другому.
|
Тем самым, Вы признаете, что верный вариант таки отличается от альтернативного?
Тогда мне непонятны Ваши претензии 
| вы ессно, можете ответить где удобней-там или здесь. мне-то все-равно. |
Тогда здесь.
Но чуть позже. |
|
|
| номер сообщения: 49-2-11203 |
|
|
|
|
| Во-вот! Наличие столь разных по степени конкретности подсказок и призвано "усреднить" эти крайности |
ыыы.. то есть для усреднения необходимо 1 задачу сформулировать примерно так-это число больше 5, а вторую-это целое число больше 5 но меньше 7. в среднем нормуль...  . мож проще дать обе сбалансированные без тыщ возможных вариантов, но в глубину? не? . мож проще дать обе сбалансированные без тыщ возможных вариантов, но в глубину? не?
Тем самым, Вы признаете, что верный вариант таки отличается от альтернативного?
Тогда мне непонятны Ваши претензии |
не понял что именно я этим признаю... что верный отличается от верного, но другого?
может я выражаюсь как-то не так... я говорю о том, что в случае верного ответа, совпавшего с авторской версией, у отвечающего нет стимула/причин искать доказательства того, что этот вариант не единственный. совпал и совпал. отлично. у нашедшего второй, тоже верный вариант, не совпавший с авторским, появляется резонное сомнение-единственный ли был вариант ответа и прав ли автор, не учевший такую возможность. не в своем ответе (иначе не давал бы его), а в правильности действий (корректности постановки и оценки задачи) автора. то есть это чисто психологический момент-если человек понимает, что его ответ удовлетворил экзаменатора на 100%, он откидывает все сомнения, если не совпадает-полезли сомнения и вопросы к задающему. нормально.
впрочем, это уже частности... не о них разговор. суть "претензий" (в вашей терминологии, по мне так это просто:
| Комментарии, замечания, объяснения, оправдания и доброжелательная (до огульности) критика приветствуются. |
)следующая:
1. между первыми подсказками типа (условно) "это число больше 0" и "этого царя прозвали грозный" логичнее выбирать что-то посреднее с ударением в сторону знаний, логики и поиска, а не множества равноценных и следовательно случайных вариантов ответов, как в 1-м (утрированном) варианте. задача типа "это может быть похоже на глагол" из этой оперы. гораздо интереснее долго и глубоко искать 1 верный вариант ответа, нежели случайно! выбирать между 10-20 тоже верными, но лежащими на поверхности и главное -совершенно равнозначными при такой абстрактной подсказке. т.е. (имхую) первая подсказка не ширь должна подразумевать/показывать вариантов, а слабодосягаемую глубь шибкую вопроса. вот и всё скромное пожелание участника. считаю оно уместное.
2. избегать по возможности задач с многозначными ответами/решениями, а поскольку гарантий таких нет ни у кого, то выработать адекватную/справедливую оценку в случае вылезшего альтернативного, но обязательно тоже верного ответа. это тоже не менее скромное скромное пожелание, не более. претензий здесь быть никаких не может в принципе, ибо мы с вами договора не подписывали, приз вы нам не обещали и доходами от тв-трансляций делиться тоже.  тут кроме благодарности трудно что-то другое высказать в целом. тут кроме благодарности трудно что-то другое высказать в целом. |
|
|
| номер сообщения: 49-2-11204 |
|
|
|
|
| rudolf: в случае вылезшего альтернативного, но обязательно тоже верного ответа. |
в игре "какое я загадал слово" не бывает альтернативных верных ответов - я какой загадал, такой и есть верный в любом случае, даже если я объяснял так криво, что никто не понял и им в голову пришли только неправильные
в случае с нашим загадывателем, однако, уже временем установлено, что объясняет он качественно, и загадки у него годные для того, что бы тратить время на их решение и получать от этого удовольствие.
за что ему и спасибо  |
|
|
| номер сообщения: 49-2-11205 |
|
|
|
|
| если я загадал слово и сделал толковую/правильную первую подсказку, что это слово из 5 букв, при этом за 1 вариант дают доп очки, а за остальные ноль, то в такую игру ломать голову не очень хоцца ибо удовольствия ноль. и я не говорю что игра хрень-наебарот, суть отличная, просто со своей колокольни советую как еще лучче сделать. а уж дело автора-внимать или посылать... |
|
|
| номер сообщения: 49-2-11206 |
|
|
|
|
| по Юрскому. считаю, что вариант Линнея тоже подходит. а)он вполне может быть лучшим среди великих биологов (первая систематизация живого мира! это практически менделеев биологии), по крайней мереон более подходит под это определение, чем чем юрский-лучший среди "комбинаторов". 1:0. б)линней-это псевдоним и тоже отца, как и у юрского.1:1 в) линней впервые научно доказывал возможность существования снежного человека и даже дал в своей систематике ему латинское название. тут тоже 1:1 г) связь с динозаврами у обоих, считаю, слишком опосредованная, но есть и там и там. у линнея по понятным причинам прямой профессии систематики животного мира, у юрского как указано. 1:1. итого у линнея если не столько же шансов, то как бы не больше. |
На мой взгляд, вышеприведенный пример - яркий образец рассуждения человека, находящегося в плену у своей гипотезы (это всем нам свойственно).
По первой подсказке: не "лучший среди комбинаторов". а "лучший среди ВЕЛИКИХ комбинаторов".
"среди великих писателей (музыкантов, ученых, футболистов)" - это просто признание заслуг. А так, в целом, ни о чем. А "среди великих комбинаторов" - это прямое указание именно на Остапа Ибрагимовича (и тех, кто его воплотил). Поэтому полагать, что по первой подсказке Линней подходит лучше... это Ваше право, конечно. Но не более того.
С симметрией во второй подсказке согласен.
Ассоциация - "Линней - снежный человек" не уступает ассоциации "Сергей Юрский - снежный человек"? Более чем сомнительный тезис.
Снежный человек - одна из первых главных ролей Юрского. Этот факт отражен во множестве источников. Да и сам фильм не раз крутили по ТВ (после того как сняли с полки).
Карл Линней, возможно интересовался снежным человеком. Но, например, в Википедии, в огромной статье про Линнея об этом нет ни слова. (Во в разы меньшей статье про Юрского "Человек ниоткуда" присутствует.)
Аналогичная ситуация с последней подсказкой. Конечно, фауна Юрского периода разнообразна. Но первая ассоциация у любого человека - динозавры (если не напрямую, то хотя бы через "Парк Юрского периода"). Ассоциация "Линней - динозавры"... А почему не лемуры, приматы, крестоцветные, пасленовые, медузы ...?
Кроме того, при правильном ответе ЮРСКИЙ в двух последних подсказках обыгрываются две совершенно разные вещи. Как и должно быть при хорошо составленных подсказках. Если же считать, что правильный ответ Линней, то две последние подсказки однотипны и откровенно плохи.
Окончательный вывод: при желании можно притянуть Линнея ко всем подсказкам. Но утверждение "итого у линнея если не столько же шансов, то как бы не больше" - это Ваше частное мнение (как будто у Вас или меня может быть какое-то иное мнение?  ) )
| -по высоцкому и батарее. вилка в 2-х значениях обыгрывается, как и многие другие слова, тоже у высоцкого. в той же песне про партию с фишером. далее-в древней игре это действительно сила-возможность атаковать 2 и более фигуры.3.точно есть в каждом доме в отличие от той же батареи. и последнее-вилочка почти всегда у человека с собой. ибо вилочка (см словари)-"Углубление в верхней части грудной кости у человека". тут тоже, считаю, промашка у вас с 2 мя подходящими значениями. |
Здесь тоже есть нюансы не в пользу ВИЛКИ. Но, поскольку в битве ЮРСКИЙ vs ЛИННЕЙ я потратил много сил, соглашусь, что здесь альтернативный вариант значительно ближе к дуали.
Но баллов не дам! 
(Про вилочку у птиц слышал. Про вилочковую железу у человека - тоже. А про вилочку у человека узнал впервые. Но в одном из пяти просмотренных мной источников такое значение таки приводится.)  |
|
|
| номер сообщения: 49-2-11207 |
|
|
|
|
- Паниковский, - сказал Остап, - вам было поручено встретиться сегодня с нашим подзащитным и вторично попросить у него миллион, сопровождая эту просьбу идиотским смехом |
|
|
| номер сообщения: 49-2-11208 |
|
|
|
|
Углубление в верхней части грудной кости у человека - почти всегда с собой?  |
|
|
| номер сообщения: 49-2-11209 |
|
|
|
|
Я, кстати, две загадки не отгадал. Мои версии выглядели надёжно, но при этом я понимал, что они, скорее всего, неверны. По опыту предыдущих конкурсов я знаю, что, когда на фоне "надёжных" версий находишь, наконец, правильную, раздаётся отчётливый звук "снап!", и всё становится на свои места. Однако, парадокс в том, что присутствие одной "очень надёжной" версии мешает найти верную.
И объективно сказать, я не припомню случая, чтобы моя последняя "очень надёжная" версия конкурировала с авторским ответом. |
|
|
| номер сообщения: 49-2-11210 |
|
|
|
|
rudolf:
Тем самым, Вы признаете, что верный вариант таки отличается от альтернативного?
Тогда мне непонятны Ваши претензии |
не понял что именно я этим признаю... что верный отличается от верного, но другого?
может я выражаюсь как-то не так... я говорю о том, что в случае верного ответа, совпавшего с авторской версией, у отвечающего нет стимула/причин искать доказательства того, что этот вариант не единственный. совпал и совпал. отлично. |
Еще раз (последний).
Раз конкурсант знает, что его ответ правильный ДО ТОГО, как опубликован разбор загадок, значит правильный таки отличается от того, который кажется ему правдоподобным.
Обратите внимание на выделенное. Ведь я (и не только я, почитайте, что roger пишет) Вам об этом толкую. А вы то ли не замечаете, то ли делаете вид, что не замечаете, этого момента. |
|
|
| номер сообщения: 49-2-11211 |
|
|
|
|
saluki:
в случае с нашим загадывателем, однако, уже временем установлено, что объясняет он качественно, и загадки у него годные для того, что бы тратить время на их решение и получать от этого удовольствие.
за что ему и спасибо  |
Спасибо за поддержку ... с довольно неожиданной стороны! |
|
|
| номер сообщения: 49-2-11212 |
|
|
|
|
| V_A_L:Спасибо за поддержку ... с довольно неожиданной стороны! |
а чего неожиданного? я всегда за хороший спорт, хотя в большинство из них не играю) |
|
|
| номер сообщения: 49-2-11213 |
|
|
|
|
А просто так: мне показалась забавной отгадка "педераст" на один из вопросов  |
|
|
| номер сообщения: 49-2-11214 |
|
|
|
|
| номер сообщения: 49-2-11221 |
|
|
|
|
У меня получается не совсем так. Мы ищем решение уравнения
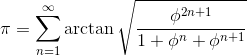
Численно у меня выходит что-то около 0.823928674, что близко к корню из пяти на е, но ему не равно. |
|
|
| номер сообщения: 49-2-11224 |
|
|
|
|
iourique: У меня получается не совсем так. Мы ищем решение уравнения
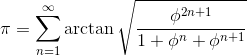
Численно у меня выходит что-то около 0.823928674, что близко к корню из пяти на е, но ему не равно. |
Я пока не понимаю, как получено это уравнение. В нём FI - величина, обратная моему PSI, так?
А что у Вас получается при малых n? Скажем, n = 3 и n = 6 - это достоверно известные случаи, должно быть 0.34601433923583 и 1.0 соответственно. |
|
|
| номер сообщения: 49-2-11225 |
|
|
|
|
Уравнение получается более не менее из теоремы косинусов. У нас есть набор треугольников с вершинами в центрах окружностей. Стороны треугольника имеют длину
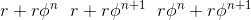
Соответственно, косинус угла при центре средней окружности равен
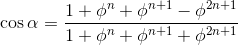
Ну и отсюда
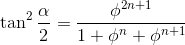
В конечных случаях надо еше отдельно рассматривать последний треугольник, так как для него формула чуть-чуть другая. Случай n = 6, впрочем, совсем простой - при phi = 1 все слагаемые равны pi/6. |
|
|
| номер сообщения: 49-2-11228 |
|
|
|
|
Вот программка на плюсах:
#include <iostream>
#include <iomanip>
#include <math.h>
double angle(double phi, int k)
{
double p = phi, sum = 0;
for (int i = 1; i < k; ++i)
{
sum += atan(p * sqrt( phi / (1 + p + p * phi) ));
p *= phi;
}
sum += atan(sqrt(p * phi / (1 + p + phi) ));
return sum - 4 * atan(1.0);
}
int main()
{
int N;
std::cout<< "Enter the number of circles: ";
std::cin>>N;
std::cout<<std::endl;
double low = 0, high = 5;
double flow = angle(low, N), fhigh = angle(high, N);
while (flow * fhigh < 0)
{
double m = 0.5 * (low + high);
double f = angle(m, N);
if (abs(f) < 1.e-16)
{
std::cout<<N<<","<<std::setprecision(16)<<1/m<<std::endl;
return 0;
}
if (f * flow > 0)
{
low = m;
flow = f;
}
else
{
high = m;
fhigh = f;
}
}
std::cout<<N<<","<<low<<std::endl;
return 0;
}
Результат:
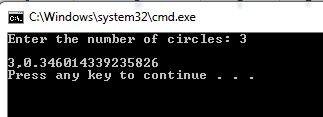
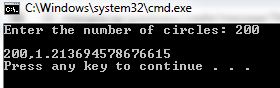 |
|
|
| номер сообщения: 49-2-11230 |
|
|
|
|
iourique: Уравнение получается более не менее из теоремы косинусов. У нас есть набор треугольников с вершинами в центрах окружностей. Стороны треугольника имеют длину
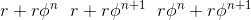
Соответственно, косинус угла при центре средней окружности равен
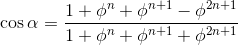
Ну и отсюда
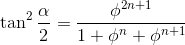
В конечных случаях надо еше отдельно рассматривать последний треугольник, так как для него формула чуть-чуть другая. Случай n = 6, впрочем, совсем простой - при \phi = 1 все слагаемые равны pi/6. |
 |
|
|
| номер сообщения: 49-2-11231 |
|
|
|
|
Я был неправ, когда написал:
ygeshelin:
Формула будет другой НЕ ТОЛЬКО для конечных случаев.
|
Ваша формула правильная. Я думаю, что при n=200 ошибка округления набегает очень сильно. Кроме того, я попробовал через арктангенс тоже, он сам даёт бОльшую ошибку, чем арккосинус.
А через арккосинус у меня получается:
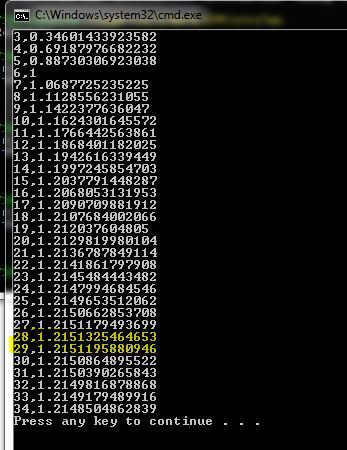
при n = 27 FI = 1.2151180505753
при n = 28 Fi = 1.2151324748993
при n = 29 Fi = 1.2151193618774
Значение e на корень из 5 = 1.2156525900874.
У Вас при n = 200 получается 1.213694578676615, т.е. отклонение от этого числа2e-3.
У меня отклонение 5e-4. Но по графику видно, что кривая ещё должна подняться чуть-чуть до ассимптоты. И тогда уже будет очень-очень точно.
Хотя, может это совпадение, конечно. Такая вычислительная казуистика...
Спасибо за программу. Могу поделиться своей на матлабе. |
|
|
| номер сообщения: 49-2-11232 |
|
|
|
|
Согласен. В районе 28 начинается фигня:
 |
|
|
| номер сообщения: 49-2-11233 |
|
|
|
|
а почем уверены в сходимости phi?  |
|
|
| номер сообщения: 49-2-11234 |
|
|
|
|
iourique: Согласен. В районе 28 начинается фигня:
 |
Проблема решаемая, конечно. Можно сконструировать какие угодно: 128- 256- ... битовые массивы и посмотреть, что будет. |
|
|
| номер сообщения: 49-2-11235 |
|
|
|
|
Хайдук: а почем уверены в сходимости phi?  |
Для начала во избежание путаницы: у меня на графике PSI, а в формулах - обратная величина, FI.
Теперь представим себе конкретный случай, например, n = 20. Двадцать окружностей уже окружают одну внутреннюю описанным способом. Добавим к ним 21-ю. Для того, чтобы соблюдалось указанное соотношение, PSI должно увеличиться, т.к. внешние круги станут чуть-чуть меньше, а внутренняя не изменится. Но именно, что чуть-чуть меньше. При n = 20 это увеличение практически незаметно и будет становиться всё меньше. Это видно на графике: функция не может не возрастать (как мы показали), но ограничена сверху пределом e на корень из 5. Взять и вдруг круто пойти вверх она тоже не может.
Не строгое рассуждение, конечно. Но строгого доказательства мы не знаем. Как не знаем, действительно ли тут e на корень из 5 или это совпадение.
Хотя, следователи, например, не верят в такие совпадения. Верят ли математики? Думаю, что нет. Например, гипотеза Коллатца по-английски так и называется: Collatz conjecture - догадка Коллатца.
https://en.wikipedia.org/wiki/Collatz_conjecture
Потому что хотя и проверена на огромных числах на суперкомпах, но строгого доказательства пока нет. |
|
|
| номер сообщения: 49-2-11236 |
|
|
|
|
| ygeshelin: функция не может не возрастать (как мы показали), но ограничена сверху пределом e на корень из 5. Взять и вдруг круто пойти вверх она тоже не может. |
что не может не возрастать не круто это ясно, но почем уверены, что e на корень из 5 будет потолком, может НЕ самым низким? если не изменяет память, сходимость можно обеспечить доказательством того, что разница psi(n+1) - psi(n) будет убывать к нулю с возрастанием числа n окружающих кругов  |
|
|
| номер сообщения: 49-2-11237 |
|
|
|
|
Хайдук:
что не может не возрастать не круто это ясно, но почем уверены, что e на корень из 5 будет потолком, может НЕ самым низким?
|
100% уверенности у меня нет, график и оценка погрешности наводят на мысль.
Хайдук:
если не изменяет память, сходимость можно обеспечить доказательством того, что разница psi(n+1) - psi(n) будет убывать к нулю с возрастанием числа n окружающих кругов  |
Так это я вроде сделал. Не знаю, насколько строго, я вообще не силён в мат доказательствах. Можно еще формализовать по методу мат индукции, но это будет то, что я написал, только с помощью формул. Помнится, к любому док-ву можно придраться, а крутые математики иногда доказывают совсем уже очевидные вещи.
То, что предел есть, более очевидно, чем то, что он е на корень из 5, ИМХО. |
|
|
| номер сообщения: 49-2-11238 |
|
|
|
|
| ygeshelin: То, что предел есть, более очевидно, чем то, что он е на корень из 5 |
пожалуй
| Хайдук: сходимость можно обеспечить доказательством того, что разница psi(n+1) - psi(n) будет убывать к нулю с возрастанием числа n окружающих кругов |
| ygeshelin: Так это я вроде сделал. Не знаю, насколько строго, я вообще не силён в мат доказательствах. Можно еще формализовать по методу мат индукции, но это будет то, что я написал, только с помощью формул. |
что не силен видно по методу мат. индукции, что тут никак НЕ пляшет 
| ygeshelin: Помнится, к любому док-ву можно придраться, а крутые математики иногда доказывают совсем уже очевидные вещи. |
далеко НЕ к любому, очевидность ошибочности НЕ в пику, а крутые математики (как Гёдель, скажем) доказать совсем уже очевидные вещи иногда НЕ могут. |
|
|
| номер сообщения: 49-2-11239 |
|
|
|
|
| К слову, фигня в районе 28 - это не численная погрешность. Ошибаться на 0.00002 в сумме из 29 слагаемых С++, а также (синхронно!) матлаб и эксель, не могут. Похоже, как это ни смешно, что последовательность немонотонна. |
|
|
| номер сообщения: 49-2-11240 |
|
|
|
|
Хайдук:
что не силен видно по методу мат. индукции, что тут никак НЕ пляшет 
|
Док-во по методу мат индукции здесь возможно. Оно состоит из трёх частей.
На 1 этапе доказывается, что утверждение истинно для n = 1. Иногда берётся 2 или более высокие значения, но тогда и всё утверждение будет доказано для любого n, начиная с этого большего числа. (У нас как раз такой случай).
На 2 втором этапе доказывается такая лемма. Пусть нам дано, что утверждение истинно для n = некому k. Тогда отсюда следует, что оно истинно для n = k + 1.
На 3 этапе мы говорим: смотрите, для 1 мы доказали? Доказали. Но тогда по лемме справедливо и для 2. Значит и для 2 доказано. Но тогда по лемме справедливо и для 3. И так без конца. Утверждение доказано.
Всё это применимо в данном случае, можно доказать, что каждое последующее увеличение FI становится меньше. Впрочем, крутые математики не считают этот метод абсолютно строгим (забыл терминологию). А вот чтобы найти значение предела, тут нужно в бесконечный ряд Тейлора разложить и вычислить сумму. Это у меня пока не получилось, впрочем, я не очень старался.
Хайдук:
| ygeshelin: Помнится, к любому док-ву можно придраться, а крутые математики иногда доказывают совсем уже очевидные вещи. |
далеко НЕ к любому, очевидность ошибочности НЕ в пику, а крутые математики (как Гёдель, скажем) доказать совсем уже очевидные вещи иногда НЕ могут. |
Я имел в виду, что доказывают, например, что между 0 и 1 есть бесконечное множество чисел. |
|
|
| номер сообщения: 49-2-11241 |
|
|
|
|
| iourique: Похоже, как это ни смешно, что последовательность немонотонна. |

ну вот видите ли, ygeshelin, может зглазили вы очевидностью той гребаной?  |
|
|
| номер сообщения: 49-2-11242 |
|
|
|
|
| iourique: Ошибаться на 0.00002 в сумме из 29 слагаемых С++, а также (синхронно!) матлаб и эксель, не могут. |
При вычислении суммы из 29 слагаемых матлаб ошибается на 1e-16. Это приводит к ошибке арккосинуса уже в 3e-08. Экспериментировал с acos(1).
Если же учесть:
- что в наших вычислениях и сам аргумент арккосинуса подбирается в результате сложных степенных вычислений, так чтобы сумма углов равнялась 2 пи с заданной точностью
- и что эта заданная точность - тоже влияющий фактор (у меня она была 1e-5),
то погрешность вполне объяснима.
| iourique: Похоже, как это ни смешно, что последовательность немонотонна. |
Будем рассуждать методом от противного. Допустим, что она не монотонна. Тогда получается, что при добавлении n+1 й окружности отношение r / R1 стало меньше, чем на предыдущем этапе. r у нас не меняется. Значит, R1 стало больше. Такого не может быть. Ведь R1, как и каждая другая внешная окружность, должно уменьшиться - иначе не втиснуть ещё одну. Значит, исходное предположение неверно. |
|
|
| номер сообщения: 49-2-11243 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2026 гг. |
|
|
|