|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| При чем тут окружность, не знаю, но задача решается элементарно. |
|
|
| номер сообщения: 49-2-11015 |
|
|
|
|
| номер сообщения: 49-2-11016 |
|
|
|
|
| Ukrfan: При чем тут окружность, не знаю, но задача решается элементарно. |
поделитесь |
|
|
| номер сообщения: 49-2-11017 |
|
|
|
|
А разве стандартная (для колпаковых задач) стратегия не проходит?
Последний называет сумму чисел на колпаках у стоящих перед ним по модулю 6 (в системе вычетов 1,2,3,4,5,6). |
|
|
| номер сообщения: 49-2-11018 |
|
|
|
|
По условию, один номер нельзя два раза называть.
У меня есть решение, я могу его Юрику в личку скинуть. |
|
|
| номер сообщения: 49-2-11019 |
|
|
|
|
iourique: | MikhailK: Я расположил числа 1-6 на окружности. Последний видит три числа. Они образуют треугольник. Тогда несложно догадаться, какое число нужно назвать, чтобы следующий точно смог назвать число на своей шляпе. |
У меня пока не получилось. |
Ясно, что вместо номеров колпаков можно использовать разные цвета, фигурки и пр. Поэтому мне подумалось, что тут должно быть чисто геометрическое, а не алгебраическое решение.
Я решал так. Расположим числа 1,2,3,4,5,6 по порядку в вершинах правильного шестиугольника. Тактику проще объяснить на примере. Пусть, например, последний видит колпаки 2-3-6. Следующий видит колпаки 3 и 6 и ему нужно как-то сообщить номер его колпака. Для этого последний называет номер 1. Нарисуйте треугольники 2-3-6 и 1-3-6. У них общее основание 3-6 (эти номера видят и последний и предпоследний), а сами треугольники являются зеркальными (получаются друг из друга отражением). Если все заранее договорились о такой стратегии, то дальше номера колпаков несложно восстанавливаются.
PS Может так получиться, что треугольник совпадает со своим зеркальным отражением (например 2-4-6). Тогда последний должен называть номер диаметрально противоположной точки (5 в данном случае).
PPS Запутанно получилось, но на самом деле просто. На картинках всё очевидно. |
|
|
| номер сообщения: 49-2-11020 |
|
|
|
|
Roger: По условию, один номер нельзя два раза называть.
|
Невнимательно прочел условие  |
|
|
| номер сообщения: 49-2-11021 |
|
|
|
|
Я Юрику сообщение не послал; у меня была, видимо, та же идея, но алгебраическая - последний вместо суммы считает число D = - c + b + а (все расчёты по модулю 6, числа для простоты я брал от 0 до 5, маленькими буквами - числа написанные, большими - вычисляемые/произносимые). Тогда очевидно, что D не может быть равно b или a (иначе два других числа тоже равны), но может быть равно c.
- Если D != c, то последний называет число D, предпоследний C = b + a - D, второй B = D + C - a, и первый A = D + C - B
- Если D = c, то поcледний вместо него называет число D = с + 3, третий считает b + a - D, получает опять D, догадывается, что что-то пошло не так, и называет число C = D + 3, далее аналогично. |
|
|
| номер сообщения: 49-2-11022 |
|
|
|
|
| такое ощущение, что вычисления вида D = - c + b + а и D = с + 3 в точности соответствуют моим геометрическим построениям |
|
|
| номер сообщения: 49-2-11023 |
|
|
|
|
| Это строго одно и то же, но без объяснения до меня геометрическая идея тоже сразу не дошла. |
|
|
| номер сообщения: 49-2-11024 |
|
|
|
|
| Давайте помедленнее. Вот, например, первый видит 2-4-6. По вашей версии он говорит 5. Тогда второй отвечает 2. А вот что делает третий? Он знает 5-2-x-6, что означает, что у него 4. Или 1. Разве нет? |
|
|
| номер сообщения: 49-2-11025 |
|
|
|
|
| iourique: Давайте помедленнее. Вот, например, первый видит 2-4-6. По вашей версии он говорит 5. Тогда второй отвечает 2. А вот что делает третий? Он знает 5-2-x-6, что означает, что у него 4. Или 1. Разве нет? |
да, есть проблема ) |
|
|
| номер сообщения: 49-2-11026 |
|
|
|
|
| LatchezarS: Каждый сообщает сумму чисел которые видит , дальше объяснения не требуются. |
Пришел Лачезар и все упростил.
Почтенный, перечитайте условия задачи, и не позорьтесь. Иногда лучше жевать, чем...
Я вот тут выше уже погорячился (имея в виду нечто среднее между решениями Валчесса и Роджера). |
|
|
| номер сообщения: 49-2-11028 |
|
|
|
|
| LatchezarS: Каждый сообщает сумму чисел которые видит , дальше объяснения не требуются. |
Еще проще составить число из цифр, которые видишь. 2-4-6? - Говоришь двести сорок шесть! 
|
|
|
| номер сообщения: 49-2-11029 |
|
|
|
|
Идея искать простое решение родила моё смехотворное и неверное решение , но вот BillyBones показал её силу.  |
|
|
| номер сообщения: 49-2-11030 |
|
|
|
|
BillyBones:
Еще проще составить число из цифр, которые видишь. 2-4-6? - Говоришь двести сорок шесть! 
|
Браво!!
Получаешь, конечно, люлей, но подельники забирают приз и компенсируют ущерб  |
|
|
| номер сообщения: 49-2-11031 |
|
|
|
|
Любопытно еще посмотреть на разные обобщения. Мое решение (видимо) обобщается на случай 4 человек и четного числа колпаков (т.е. числа на колпаках могут быть от 1 до 2n).
При этом задача с 4 людьми и 5 колпаками допускает единственную стратегию и она непохожа на случай 6 колпаков.
Задача с 6 людьми и 12 колпаками решается через систему Штейнера S(5,6,12). Но может можно и проще. |
|
|
| номер сообщения: 49-2-11032 |
|
|
|
|
| номер сообщения: 49-2-11033 |
|
|
|
|
Ukrfan: BillyBones:
Еще проще составить число из цифр, которые видишь. 2-4-6? - Говоришь двести сорок шесть! 
|
Браво!!
Получаешь, конечно, люлей, но подельники забирают приз и компенсируют ущерб  |
Увы, в оригинале требовалось называть "числа от 1 до 6". В переводе на русский это ограничение как то пропало. |
|
|
| номер сообщения: 49-2-11034 |
|
|
|
|
| Barsoom:Увы, в оригинале требовалось называть "числа от 1 до 6". В переводе на русский это ограничение как то пропало. |
да все понятно, кэп! :) "куда-то пропало" ваше чувство юмора, которого обычно вам не занимать. |
|
|
| номер сообщения: 49-2-11035 |
|
|
|
|
Еще задачку подкину. Решения не знаю, надеюсь на помощь клуба.
6 точек попарно соединены стрелками, всего 30 стрелок. Можно ли их разбить на 6 циклов длины 5? (Разумеется, каждая стрелка должна принадлежать ровно одному циклу и все стрелки в цикле должны быть направлены в одну сторону.) |
|
|
| номер сообщения: 49-2-11036 |
|
|
|
|
| Как я понимаю, условие не запрещает проходить через одну точку в цикле дважды? Тогда можно. |
|
|
| номер сообщения: 49-2-11038 |
|
|
|
|
| Roger: Как я понимаю, условие не запрещает проходить через одну точку в цикле дважды? Тогда можно. |
Вообще-то запрещает, это я забыл упомянуть. |
|
|
| номер сообщения: 49-2-11039 |
|
|
|
|
| Я сразу заподозрил неладное. |
|
|
| номер сообщения: 49-2-11040 |
|
|
|
|
Я, впрочем, и в упрощенном случае решения не знаю, но я над ним почти не думал.
p.s. уже знаю. |
|
|
| номер сообщения: 49-2-11041 |
|
|
|
|
| номер сообщения: 49-2-11042 |
|
|
|
|
| Roger: Я сразу заподозрил неладное. |
А все равно можно. Оказалось, что надо было сменить парадигму - я думал про 6-угольник, а нужно было думать про 5-угольник с центром. |
|
|
| номер сообщения: 49-2-11043 |
|
|
|
|
| На предыдущей задаче я застрял, но Вы пока не пишите ответ. |
|
|
| номер сообщения: 49-2-11044 |
|
|
|
|
ненавижу думать  , go get it, guys! , go get it, guys! |
|
|
| номер сообщения: 49-2-11045 |
|
|
|
|
Я пока поговорю про задачку с циклами.
Если заменить 6 на 5 решение существенно упрощается:
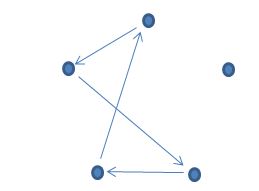
Осталось повернуть этот цикл на пятую часть окружности 4 раза.
Забавным образом превратить это решение в решении для 6 точек почти ничего не стоит:
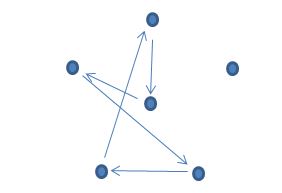
Этот цикл тоже надо повернуть 4 раза и добавить один внешний цикл. |
|
|
| номер сообщения: 49-2-11050 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2025 гг. |
|

|
|