|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
V_A_L: | Pirron: Мало было темы про головоломки - теперь еще новую открыли... Чувствуешь себя каким-то идиотом. |
... то есть, примерно так, как буду чувствовать себя я, сев играть в шахматы со многими из обитателей chesspro.
Хоть тут отыграться!  |
Простите, вы Ослика не прокомментировали... Что, совсем плохо?.. |
|
|
| номер сообщения: 49-19-2419 |
|
|
|
|
Sad_Donkey: V_A_L: | Pirron: Мало было темы про головоломки - теперь еще новую открыли... Чувствуешь себя каким-то идиотом. |
... то есть, примерно так, как буду чувствовать себя я, сев играть в шахматы со многими из обитателей chesspro.
Хоть тут отыграться!  |
Простите, вы Ослика не прокомментировали... Что, совсем плохо?.. |
Ваша стратегия дает в точности 1/2. |
|
|
| номер сообщения: 49-19-2420 |
|
|
|
|
iourique: Sad_Donkey: V_A_L: | Pirron: Мало было темы про головоломки - теперь еще новую открыли... Чувствуешь себя каким-то идиотом. |
... то есть, примерно так, как буду чувствовать себя я, сев играть в шахматы со многими из обитателей chesspro.
Хоть тут отыграться!  |
Простите, вы Ослика не прокомментировали... Что, совсем плохо?.. |
Ваша стратегия дает в точности 1/2. |
Ну, по крайней мере, я, стало быть, утверждал, что вторым быть - не хуже... Не так уж и плохо... |
|
|
| номер сообщения: 49-19-2421 |
|
|
|
|
Sad_Donkey:
Простите, вы Ослика не прокомментировали... Что, совсем плохо?.. |
Вы ведь сами прокомментировали. Я полагал, что этого достаточно 
А если серьезно, Вы правы, утверждая, что второму игроку игра выгодна. Но предложенная стратегия позволяет ему иметь шансы 50%. В то время как у него (как верно заметил iourique всегда есть комбинация, по крайней мере, на 62.5% (а если А сглупит, то и на все 87.5%)
Опять опередили  Надо осваивать двадцатипальцевый метод. Надо осваивать двадцатипальцевый метод. |
|
|
| номер сообщения: 49-19-2422 |
|
|
|
|
V_A_L: Sad_Donkey:
Простите, вы Ослика не прокомментировали... Что, совсем плохо?.. |
Вы ведь сами прокомментировали. Я полагал, что этого достаточно 
А если серьезно, Вы правы, утверждая, что второму игроку игра выгодна. Но предложенная стратегия позволяет ему иметь шансы 50%. В то время как у него (как верно заметил iourique всегда есть комбинация, по крайней мере, на 62.5% (а если А сглупит, то и на все 87.5%)
Опять опередили  Надо осваивать двадцатипальцевый метод. Надо осваивать двадцатипальцевый метод. |
Хорошо спасибо. Полагаю, по системе зачета: "время ответа + качество ответа" я, в этот раз, был не последним. Я сразу чего-то "вякнул" и потом и не думал; и вообще ничего не считал... |
|
|
| номер сообщения: 49-19-2423 |
|
|
|
|
| номер сообщения: 49-19-2424 |
|
|
|
|
Вот еще один парадокс (уже, кажется, на этом или каком-то предшествующем форуме обсуждавшийся). Для тех, кто считает, что если вероятности неизвестны, то они наверное равны.
Человеку предлагают на выбор два конверта, сообщая, что в одном из них денег вдвое больше, чем в другом. После того, как человек выбрал конверт, но до того, как он его открыл, ему предлагают поменять конверт на другой. Его рассуждения: "С вероятностью 1/2 я выбрал конверт, в котором меньше (больше) денег. Пусть в моем конверте $n, тогда во втором либо n/2, либо 2n. Матожидание при обмене 1/2 * n/2 + 1/2 * 2n = 5/4 n, что больше, чем n. Надо меняться!". |
|
|
| номер сообщения: 49-19-2425 |
|
|
|
|
На предыдущей задаче можно тестировать генераторы псевдослучайных чисел.
Вот, например, "плохой" генератор из стандартной библиотеки (примерно миллион событий на каждый случай):
OOO OOP OPO OPP POO POP PPO PPP
OOO XXXXX 0.504 0.380 0.388 0.106 0.403 0.316 0.501
OOP 0.496 XXXXX 0.672 0.657 0.267 0.637 0.502 0.677
OPO 0.620 0.328 XXXXX 0.503 0.493 0.513 0.355 0.568
OPP 0.612 0.343 0.497 XXXXX 0.493 0.508 0.733 0.871
POO 0.894 0.733 0.507 0.507 XXXXX 0.509 0.338 0.598
POP 0.597 0.363 0.487 0.492 0.491 XXXXX 0.331 0.595
PPO 0.684 0.498 0.645 0.267 0.662 0.669 XXXXX 0.516
PPP 0.499 0.323 0.432 0.129 0.402 0.405 0.484 XXXXX
А вот "хороший" генератор Ranlux.
OOO OOP OPO OPP POO POP PPO PPP
OOO XXXXX 0.500 0.400 0.400 0.125 0.417 0.300 0.500
OOP 0.500 XXXXX 0.666 0.667 0.251 0.625 0.500 0.701
OPO 0.600 0.334 XXXXX 0.499 0.500 0.500 0.375 0.583
OPP 0.600 0.333 0.501 XXXXX 0.499 0.500 0.750 0.875
POO 0.875 0.749 0.500 0.501 XXXXX 0.500 0.334 0.600
POP 0.583 0.375 0.500 0.500 0.500 XXXXX 0.333 0.601
PPO 0.700 0.500 0.625 0.250 0.666 0.667 XXXXX 0.500
PPP 0.500 0.299 0.417 0.125 0.400 0.399 0.500 XXXXX
|
|
|
| номер сообщения: 49-19-2426 |
|
|
|
|
iourique: Вот еще один парадокс (уже, кажется, на этом или каком-то предшествующем форуме обсуждавшийся). Для тех, кто считает, что если вероятности неизвестны, то они наверное равны.
Человеку предлагают на выбор два конверта, сообщая, что в одном из них денег вдвое больше, чем в другом. После того, как человек выбрал конверт, но до того, как он его открыл, ему предлагают поменять конверт на другой. Его рассуждения: "С вероятностью 1/2 я выбрал конверт, в котором меньше (больше) денег. Пусть в моем конверте $n, тогда во втором либо n/2, либо 2n. Матожидание при обмене 1/2 * n/2 + 1/2 * 2n = 5/4 n, что больше, чем n. Надо меняться!". |
Очень красиво. Мне кажется, эту задачу лучше дать с чуть измененной формулировкой: мы не только выбрали конверт, но и открыли его и увидели эти n денег. Во втором конверте по-прежнему вдвое больше или вдвое меньше денег, мы не знаем сколько. Дальнейшие рассуждения - аналогичны. У меня возникла некая аналогия из квантовой механики. Тут видно, что мы провели "измерение" и перешли из состояния суперпозиции в "чистое" состояние (пусть и неясно какое). Видимо, уже это дает нам некую информацию? |
|
|
| номер сообщения: 49-19-2427 |
|
|
|
|
| Расскажите, в чем тут дело! :) |
|
|
| номер сообщения: 49-19-2428 |
|
|
|
|
| iourique: Вот еще один парадокс (уже, кажется, на этом или каком-то предшествующем форуме обсуждавшийся). |
Угу. Только что обсуждалось на dxdy. А кроме того, есть в Википедии (см. "Задача о двух конвертах")
Для тех, кто считает, что если вероятности неизвестны, то они наверное равны.
Человеку предлагают на выбор два конверта, сообщая, что в одном из них денег вдвое больше, чем в другом. После того, как человек выбрал конверт, но до того, как он его открыл, ему предлагают поменять конверт на другой. Его рассуждения: "С вероятностью 1/2 я выбрал конверт, в котором меньше (больше) денег. Пусть в моем конверте $n, тогда во втором либо n/2, либо 2n. Матожидание при обмене 1/2 * n/2 + 1/2 * 2n = 5/4 n, что больше, чем n. Надо меняться!". |
Кстати, Гарднер признавался, что он так и не понял окончательно объяснение этого парадокса. |
|
|
| номер сообщения: 49-19-2429 |
|
|
|
|
| В своё время мы с Сашей из Виннипега его добили :-) Там по ходу надо разбираться с самим понятием вероятности, и оказывается, кстати, что задачу можно понимать минимум 2-мя различными способами(что впрочем, кажется не влияет на ответ). |
|
|
| номер сообщения: 49-19-2430 |
|
|
|
|
Увидел пост Жени. Вот тут:
http://www.guestbook.ru/?user=KasparovChess&page=15&language=russian
начиная с поста 30623
И дальше посты 30680 30683, 30713, 30734, 30737, 30738 |
|
|
| номер сообщения: 49-19-2431 |
|
|
|
|
| jenya: Расскажите, в чем тут дело! :) |
Приблизительно так: изначальная посылка, что он с равной вероятностью хапнул либо конверт с большей суммой, либо с меньшей, очевидно верна. А вот как только он предполагает, что у него в конверте $n, сказка неожиданно заканчивается.
Действительно, предположим в конвертах может лежать $2^k и пусть p_k - вероятность того, что в конвертах 2^k и 2^{k+1} (k бежит от минус бесконечности до плюс бесконечности). Если бы все p_k были равны, наш герой оказался бы прав - но таких распределений не бывает. Это означает, что как он только он предположил (или заглянул и увидел), что у него в конверте 2^k, вероятности поменялись (превратились в условные вероятности). Теперь вероятность, что он тяпнул большую сумму p_{k-1}/(p_{k-1}+p_k), что вообще говоря совсем не 1/2. Матожидание обмена:
2^{k-1} p_{k-1}/(p_{k-1}+p_k) + 2^{k+1} p_k/(p_{k-1}+p_k).
Просуммировав по k с правильными весами, легко убедиться, что оно в среднем не изменилось по сравнению с ситуацией до обмена. |
|
|
| номер сообщения: 49-19-2432 |
|
|
|
|
| Моё решение иное. Вы решаете формализованную задачу с действительно бесконечным количеством конвертов и платите за это отказом от равной вероятности конвертов. Мне это решительно не нравится :-) |
|
|
| номер сообщения: 49-19-2433 |
|
|
|
|
| Grigoriy: Моё решение иное. Вы решаете формализованную задачу с действительно бесконечным количеством конвертов и платите за это отказом от равной вероятности конвертов. Мне это решительно не нравится :-) |
Григорий, Вы, по-моему, забываете, что вероятности могут быть нулевыми :) так что конечность/бесконечность неважна. |
|
|
| номер сообщения: 49-19-2434 |
|
|
|
|
| Я решал задачу именно с равными вероятностями, так что от бесконечного числа конвертов мне пришлось отказаться(впрочем, не только потому и это была не самая важная причина - были более глубокие основания). Саша разобрал и случай разных вероятностей. |
|
|
| номер сообщения: 49-19-2435 |
|
|
|
|
| Grigoriy: Я решал задачу именно с равными вероятностями, так что от бесконечного числа конвертов мне пришлось отказаться(впрочем, не только потому и это была не самая важная причина - были более глубокие основания). Саша разобрал и случай разных вероятностей. |
Решение, которое я привел (не мое) - общее. Если хотите конечное число конвертов с равными вероятностями, то положите p_1=p_2=..=p_n=1/n, p_i = 0 для остальных i. Идея ровно та же - где-то случается перепад вероятностей (в данном случае на краях), там-то и прячется ошибка в изначальном рассуждении. |
|
|
| номер сообщения: 49-19-2436 |
|
|
|
|
| Консенсус :-) Но всё-таки, моё решение мне нравится больше :-) Вот почему: там разбирается смысл понятия вероятности в данном случае - что не совсем тривиально. Т е там я разбираюсь по существу, и выдаю рецепт, как действовать :-) |
|
|
| номер сообщения: 49-19-2437 |
|
|
|
|
| Интересно, что на это сообщение никто не отреагировал: на мой взгляд, конверты по сравнению с этим - детский лепет. |
|
|
| номер сообщения: 49-19-2439 |
|
|
|
|
| Вспомнил еще один результат, который довольно сложно переварить. Вопрос: сколько должно быть человек в компании, чтобы с вероятностью большей 1/2 у каких-нибудь двух из них совпадали дни рождения? Незнающим предлагается сначаль дать интуитивную оценку, а уже потом решать. |
|
|
| номер сообщения: 49-19-2499 |
|
|
|
|
| iourique: Вспомнил еще один результат, который довольно сложно переварить. Вопрос: сколько должно быть человек в компании, чтобы с вероятностью большей 1/2 у каких-нибудь двух из них совпадали дни рождения? Незнающим предлагается сначаль дать интуитивную оценку, а уже потом решать. |
Интуитивную совсем легко - в классах по 30-40человек совпадение как правило было. Я бы дал 30 интуитивно |
|
|
| номер сообщения: 49-19-2502 |
|
|
|
|
| iourique: Вспомнил еще один результат, который довольно сложно переварить. Вопрос: сколько должно быть человек в компании, чтобы с вероятностью большей 1/2 у каких-нибудь двух из них совпадали дни рождения? Незнающим предлагается сначаль дать интуитивную оценку, а уже потом решать. |
При равномерном распределении? |
|
|
| номер сообщения: 49-19-2503 |
|
|
|
|
Sad_Donkey: | iourique: Вспомнил еще один результат, который довольно сложно переварить. Вопрос: сколько должно быть человек в компании, чтобы с вероятностью большей 1/2 у каких-нибудь двух из них совпадали дни рождения? Незнающим предлагается сначаль дать интуитивную оценку, а уже потом решать. |
При равномерном распределении? |
Угу. |
|
|
| номер сообщения: 49-19-2504 |
|
|
|
|
bazar: | iourique: Вспомнил еще один результат, который довольно сложно переварить. Вопрос: сколько должно быть человек в компании, чтобы с вероятностью большей 1/2 у каких-нибудь двух из них совпадали дни рождения? Незнающим предлагается сначаль дать интуитивную оценку, а уже потом решать. |
Интуитивную совсем легко - в классах по 30-40человек совпадение как правило было. Я бы дал 30 интуитивно |
Неплохо. |
|
|
| номер сообщения: 49-19-2505 |
|
|
|
|
iourique: | Sad_Donkey: При равномерном распределении? |
Угу. |
По поводу равномерного распределения и причин его нарушения - Winter blackout results in Dutch baby boom.
Вкратце - в нескольких деревнях Голландии зафиксирован подъём рождаемости через 9 месяцев после двухдневного отключения электроэнергии. Статистическая подтверждённость, правда, плохая. |
|
|
| номер сообщения: 49-19-2506 |
|
|
|
|
iourique: bazar: | iourique: Вспомнил еще один результат, который довольно сложно переварить. Вопрос: сколько должно быть человек в компании, чтобы с вероятностью большей 1/2 у каких-нибудь двух из них совпадали дни рождения? Незнающим предлагается сначаль дать интуитивную оценку, а уже потом решать. |
Интуитивную совсем легко - в классах по 30-40человек совпадение как правило было. Я бы дал 30 интуитивно |
Неплохо. |
У меня - 19. Кто меньше? |
|
|
| номер сообщения: 49-19-2507 |
|
|
|
|
| Sad_Donkey: У меня - 19. Кто меньше? |
Парадокс дней рождения
Эта статья входит в число хороших статей русскоязычного раздела Википедии
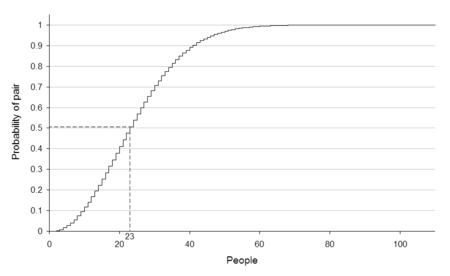
График показывает вероятность того, что у каких-нибудь двух человек из группы совпадут дни рождения. |
|
|
| номер сообщения: 49-19-2508 |
|
|
|
|
MikhailK: | Sad_Donkey: У меня - 19. Кто меньше? |
Парадокс дней рождения
Эта статья входит в число хороших статей русскоязычного раздела Википедии

График показывает вероятность того, что у каких-нибудь двух человек из группы совпадут дни рождения. |
Посмотрел. У меня речь идет том, сколько человек минимум должно быть (оценка), чтобы вероятность события "нет совпадающих дней рождения" была больше половины... |
|
|
| номер сообщения: 49-19-2509 |
|
|
|
|
| Сэд, это, вроде, одно и то же? |
|
|
| номер сообщения: 49-19-2510 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|