|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| iourique: Я не знаю точно, больше ли их, чем континуум. |
Уже знаю. Не больше. Функции из N в N можно рассматривать как (довольно специальные) подмножества в N х N. Так как N х N = N, а множество подмножеств натуральных чисел равномощно множеству действительных чисел, то отображений из N в N не больше, чем действительных числе. С другой стороны, если нам дано иррациональное число 0<а<1 в двоичной записи, то по нему легко можно построить биекцию f из N в N: f(n) = 2k, если n-ый знак а равен 0 и среди первых n знаков а k нулей, и f(n)=2k-1, если n-ый знак а равен 1 и среди первых n знаков а k единиц. Следовательно, иррациональных чисел не больше, чем биекций из N в N. |
|
|
| номер сообщения: 49-2-2909 |
|
|
|
|
iourique: | MikhailK: Осталось теперь туда впихнуть все остальные алгебраические числа. |
А как их туда впихивать? |
Мне кажется, что я придумал вполне строгое, но немного корявое построение. Занумеруем все алгебраические числа. Возьмём теперь произвольное трансцендентное число. Оно является числом-антидиагональю некоторого счетного упорядоченного набора алгебраических чисел.
Возьмем теперь первое алгебраическое число (мы же их занумеровали). Если оно уже использовано в построении трансцендентного числа, то ничего не делаем. В противном случае попробуем его вставить в канторово построение на место другого числа. Такое место всегда найдется. Пусть оно оказалось на строке k_1. Поместим туда первое число.
Возьмем теперь второе алгебраическое число (мы же их занумеровали). Если оно уже использовано в построении трансцендентного числа, то ничего не делаем. В противном случае попробуем его вставить в канторово построение на место другого числа, причем подходящее место будем искать начиная со строки k_1. Такое место всегда найдется. Пусть оно оказалось на строке k_2. Поместим туда второе число.
....
Возьмем теперь m-тое алгебраическое число (мы же их занумеровали). Если оно уже использовано в построении трансцендентного числа, то ничего не делаем. В противном случае попробуем его вставить в канторово построение на место другого числа, причем подходящее место будем искать начиная со строки k_{m-1}. Если на подходящем месте окажется число с номером меньшим m, то ищем дальше. Рано или поздно подходящее место найдется. Пусть оно оказалось на строке k_m. Поместим туда m-тое число.
Таким способом можно запихнуть в канторово построение данного трансцендентного числа все алгебраические числа.
Очень надеюсь, что мне удалось донести свою мысль. Уверен, что построение можно значительно упростить. |
|
|
| номер сообщения: 49-2-2910 |
|
|
|
|
MikhailK: iourique: | MikhailK: Осталось теперь туда впихнуть все остальные алгебраические числа. |
А как их туда впихивать? |
Мне кажется, что я придумал вполне строгое, но немного корявое построение.
|
Похоже, что работает. Здорово. Да и не такое оно корявое. Начинаем с какой-то таблицы, выбираем произвольное число М. Бежим по списку алгебраических чисел. Если текущее число уже в таблице, то присваиваем М значение, равное максимуму из М и номера этого числа в таблице, переходим к следующему, если нет - вставляем на первое подходящее место после М, присваиваем М номер этого места, переходим к следующему. Таким образом, уже обслуженные числа из таблицы не выкидываются и каждое число в нее попадает. |
|
|
| номер сообщения: 49-2-2911 |
|
|
|
|
iourique:
Это - классика. По-моему, здесь даже когда-то обсуждалось.
Задача 3
Эта задача является гибридом предыдущих. Пусть мудрецы стоят в шеренгу, колпаки q цветов случайным образом одеты на головы мудрецов, мудрецы видят только колпаки впередистоящих, разрешено пасовать. Как и в задаче 1 мудрецы пытаются по очереди угадать цвет своего колпака (или пасовать) и при этом слышат предположения стоящих позади мудрецов. Цель - угадать цвет хотя бы одного колпака и ни разу не ошибиться.
Какова оптимальная стратегия? |
Сходу в голову не приходит ничего умнее такой стратегии: [...] |
Первая задача действительно классика. Но ведь третья от нее практически не отличается.
Вновь можно гарантировать, что все мудрецы правильно назовут цвета своих колпаков, за исключением, разве что, стоящего последним (и говорящего первым).
Причем стратегия практически не отличается от своего аналога для случая двух цветов. Только рассуждение (подсчет цвета своего колпака) ведется не по модулю 2, а по модулю q. |
|
|
| номер сообщения: 49-2-2912 |
|
|
|
|
V_A_L:
Первая задача действительно классика. Но ведь третья от нее практически не отличается. |
Вы, кажется, невнимательно прочитали условие - в третьей задаче нужно, чтобы никто не ошибся и хотя бы кто-нибудь угадал. Стратегия первой задачи дает ужасный результат - вероятность успеха 1/q. |
|
|
| номер сообщения: 49-2-2913 |
|
|
|
|
iourique: V_A_L:
Первая задача действительно классика. Но ведь третья от нее практически не отличается. |
Вы, кажется, невнимательно прочитали условие - в третьей задаче нужно, чтобы никто не ошибся и хотя бы кто-нибудь угадал. Стратегия первой задачи дает ужасный результат - вероятность успеха 1/q. |
Вам правильно кажется :)
Прочитал по диагонали и "увидел" (а на самом деле вспомнил) другую задачу. |
|
|
| номер сообщения: 49-2-2934 |
|
|
|
|
iourique:
Задача 3
Эта задача является гибридом предыдущих. Пусть мудрецы стоят в шеренгу, колпаки q цветов случайным образом одеты на головы мудрецов, мудрецы видят только колпаки впередистоящих, разрешено пасовать. Как и в задаче 1 мудрецы пытаются по очереди угадать цвет своего колпака (или пасовать) и при этом слышат предположения стоящих позади мудрецов. Цель - угадать цвет хотя бы одного колпака и ни разу не ошибиться.
Какова оптимальная стратегия? |
Сходу в голову не приходит ничего умнее такой стратегии: последний (тот, клму всех видно) пасует, если колпаков белого цвета не меньше, чем колпаков любого другого. Остальные пасуют, если этой информации им не хватает. Рано или поздно один из носителей белого колпака сообразит. Если же белых колпаков меньше, чем, например, черных, последний называет цвет наугад. Ну и разумеется, как только кто-то что-то сказал, остальные пасуют. Наверно, можно и лучше... |
Делаю еще одну попытку высказаться. Если я опять что-то напутал, не судите строго 
Каждый мудрец, начиная с последнего пасует, если видит перед собой хотя бы один белый колпак, и говорит "белый" в противном случае.
Чем больше мудрецов и чем меньше цветов, тем эффективнее стратегия. |
|
|
| номер сообщения: 49-2-2935 |
|
|
|
|
В процессе работы приходится постоянно работать с матрицами размером 2x2. При этом в промежуточных выкладках появляются громоздкие выражения, которые при явном покомпонентном вычислении оказываются тривиальными. Например, обнаружился следующий факт, который я сформулирую в виде простой задачи.
Пусть A,B,C - три произвольные матрицы размером 2x2, у которых сумма диагональных элементов равно нулю (бесследовая матрица). Необходимо вычислить следующее выражение
ABC-CBA
Чему оно равно и почему?
PS Знакомые алгебраисты немного подумали и сказали, что ответ понятен и очевиден. Я теперь тоже его понимаю, но интуиция в подобных штуках у меня пока плохо развита. Интересно, что нужно сделать, чтобы подобные комбинации видеть сразу?
PPS Я тут подумал, что всю мою научную деятельность можно охарактеризовать довольно смешно. Я извлекаю корни из единичной матрицы (Quantrinas поймет). |
|
|
| номер сообщения: 49-2-2936 |
|
|
|
|
MikhailK: В процессе работы приходится постоянно работать с матрицами размером 2x2. При этом в промежуточных выкладках появляются громоздкие выражения, которые при явном покомпонентном вычислении оказываются тривиальными. Например, обнаружился следующий факт, который я сформулирую в виде простой задачи.
Пусть A,B,C - три произвольные матрицы размером 2x2, у которых сумма диагональных элементов равно нулю (бесследовая матрица). Необходимо вычислить следующее выражение
ABC-CBA
Чему оно равно и почему?
|
Скалярная матрица получается, однако.
PS Знакомые алгебраисты немного подумали и сказали, что ответ понятен и очевиден. |
Я не думал, просто посчитал в общем виде.
А как Ваши знакомые объясняют этот эффект без вычислений? |
|
|
| номер сообщения: 49-2-2937 |
|
|
|
|
| V_A_L: А как Ваши знакомые объясняют этот эффект без вычислений? |
Мне тоже интересно. У меня получилось только рассуждение в духе матриц Паули (примерно так: без ограничения общности можно считать В диагональной, а А - внедиагональной, а С разбить на диагональную и внедиагональную часть, после чего все либо коммутирует, либо антикоммутирует), но это все равно выглядит довольно громоздко и не вполне очевидно. |
|
|
| номер сообщения: 49-2-2938 |
|
|
|
|
Рассуждение были основаны на том, что в пространстве матриц 2x2 справедливы следующие утверждения
1) произведение бесследовой матрицы на единичный антисимметричный тензор дает симметричную матрицу.
2) пространство антисимметричных матриц одномерно и состоит из матриц кратных единичному антисимметричному тензору
Дальше все просто. Пусть e - единичный антисимметричный тензор, тогда запишем следующую цепочку равенств
ABC-CBA=AeeBeeCee-CeeBeeAee=((Ae)e(Be)e(Ce)-(Ce)e(Be)e(Ae))e=De,
где
D=(Ae)e(Be)e(Ce)-(Ce)e(Be)e(Ae)
Отметим, что матрицы (Ae), (Be) и (Ce) симметричные, а матрица e - антисимметричная. Отсюда немедленно следует, что матрица D - антисимметрична. Значит она кратна единичному антисимметричному тензору, и следовательно De - скалярная матрица. |
|
|
| номер сообщения: 49-2-2939 |
|
|
|
|
Блин, я преклоняюсь перед людьми, для которых это - очевидно.  |
|
|
| номер сообщения: 49-2-2940 |
|
|
|
|
iourique: Блин, я преклоняюсь перед людьми, для которых это - очевидно.  |
У них переход от бесследовых матриц 2x2 к симметричным на уровне рефлексов, а далее уже легко. |
|
|
| номер сообщения: 49-2-2941 |
|
|
|
|
MikhailK: iourique: Блин, я преклоняюсь перед людьми, для которых это - очевидно.  |
У них переход от бесследовых матриц 2x2 к симметричным на уровне рефлексов, а далее уже легко. |
Меня, наверно, смущает, что это какой-то сугубо двумерный эфеект. Или есть какие-нибудь обобщения на матрицы большей размерности? Впрочем, sl_2 - полезный объект. |
|
|
| номер сообщения: 49-2-2942 |
|
|
|
|
| iourique: Меня, наверно, смущает, что это какой-то сугубо двумерный эфеект. Или есть какие-нибудь обобщения на матрицы большей размерности? Впрочем, sl_2 - полезный объект. |
Да, это свойство именно матриц 2x2. |
|
|
| номер сообщения: 49-2-2943 |
|
|
|
|
| Пусть р - наименьшее простое число, делящее порядок конечной группы G, Н - подгруппа индекса р. Доказать, что Н нормальна в G |
|
|
| номер сообщения: 49-2-2946 |
|
|
|
|
MikhailK: Рассуждение были основаны на том, что в пространстве матриц 2x2 справедливы следующие утверждения
1) произведение бесследовой матрицы на единичный антисимметричный тензор дает симметричную матрицу.
2) пространство антисимметричных матриц одномерно и состоит из матриц кратных единичному антисимметричному тензору
|
Пока был в отпуске немного думал на эту тему. Если отвлечься от размерности 2, то остаются следующие забавный факты:
1) произведение симметрической и кососимметрической матриц имеет след 0 [tr(SA) = tr(AS) = tr((AS)^t) = - tr(SA)];
2) матрицы вида SA, где А - фиксированная кососимметрическая матрица, а S пробегает все симметрические матрицы (или наоборот, А пробегает все кососимметрические, а S - фиксированная симметрическая) образуют алгебру Ли, так как
(а) [S_1 A, S_2 A] = S_1 A S_2 A - S_2 A S_1 A = (S_1 A S_2 - S_2 A S_1)A, а матрица S_1 A S_2 - S_2 A S_1 - симметрическая, или
(б) [S A_1, S A_2] = S A_1 S A_2 - S A_2 S A_1 = S(А_1 S А_2 - A_2 S A_1), а матрица А_1 S А_2 - A_2 S A_1 - кососимметрическая.
Факт 2) вроде бы очень простенький, но не помню, что бы я о нем слышал. Интересно, что это за алгебра Ли. Тривиальный частный случай утверждения 2б) заключается в том, что множество кососимметрических матриц образует алгебру Ли so(n). Она является алгеброй Ли для группы SO(n) ортогональных матриц. |
|
|
| номер сообщения: 49-2-2947 |
|
|
|
|
Человек сегодня на интервью пришел. Цитата из резюме:
"Over nine papers published or accepted in top mathematics journals".
Безуспешно пытаюсь придти в себя. |
|
|
| номер сообщения: 49-2-2951 |
|
|
|
|
iourique: Человек сегодня на интервью пришел. Цитата из резюме:
"Over nine papers published or accepted in top mathematics journals".
Безуспешно пытаюсь придти в себя. |
10?
Раз уж тема поднялась, то расскажу о сегодняшнем открытии. Пусть A,B,C,D - произвольные бесследовые матрицы 2x2. Рассмотрим величину
tr(ABCD)
Из физических соображений мне хотелось, чтобы эта величина не менялась при перестановке матриц B и D. Несложно установить, что это действительно так и является элементарным следствием из предыдущего утверждения. |
|
|
| номер сообщения: 49-2-2952 |
|
|
|
|
iourique: Человек сегодня на интервью пришел. Цитата из резюме:
"Over nine papers published or accepted in top mathematics journals".
Безуспешно пытаюсь придти в себя. |
А что - двузначное число статей, это красиво.
Может их и больше чем 10.
Например, 11 или 12.
Говорят же дамы про свой возраст - мне тридцать с хвостиком (а хвостик тянет еще на 15). |
|
|
| номер сообщения: 49-2-2953 |
|
|
|
|
Попалась действительно забавная задача.
Имеется треугольный торт и треугольная коробка к нему.

Длины сторон торта совпадают с длинами сторон коробки, но, как видно из рисунка, просто так торт в коробку не положить.
На сколько кусков нужно разрезать торт, чтобы упаковать его в коробку. Переворачивать куски торта кремом вниз нельзя.
PS В исходной формулировке спрашивалось о количестве кусков. Мне кажется, что также интересно подумать о количестве прямолинейных разрезов (не обязательно от края до края торта), необходимых для укладки торта в коробку. |
|
|
| номер сообщения: 49-2-2963 |
|
|
|
|
MikhailK: Попалась действительно забавная задача.
Имеется треугольный торт и треугольная коробка к нему.

Длины сторон торта совпадают с длинами сторон коробки, но, как видно из рисунка, просто так торт в коробку не положить.
На сколько кусков нужно разрезать торт, чтобы упаковать его в коробку. Переворачивать куски торта кремом вниз нельзя.
PS В исходной формулировке спрашивалось о количестве кусков. Мне кажется, что также интересно подумать о количестве прямолинейных разрезов (не обязательно от края до края торта), необходимых для укладки торта в коробку. |
Мысли вслух - с кусками вроде просто, ответ: 3. Двух кусков (одного разреза) хватает только на специальные треугольники - прямоугольные или с углами 180-х, 180-2х, 3х-180. На три куска можно разрезать всегда (тремя разрезами). Остается вопрос, к которому я даже не знаю, с какой стороны подойти - можно ли обойтись двумя разрезами? |
|
|
| номер сообщения: 49-2-2964 |
|
|
|
|
iourique:
Мысли вслух - с кусками вроде просто, ответ: 3. Двух кусков (одного разреза) хватает только на специальные треугольники - прямоугольные или с углами 180-х, 180-2х, 3х-180. На три куска можно разрезать всегда (тремя разрезами). Остается вопрос, к которому я даже не знаю, с какой стороны подойти - можно ли обойтись двумя разрезами? |
Если минимизировать число кусков, то ответ вот такой
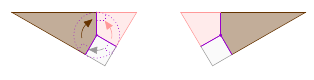
Любопытно, что нижеперечисленные торты для укладки в коробку достаточно разрезать на два куска.
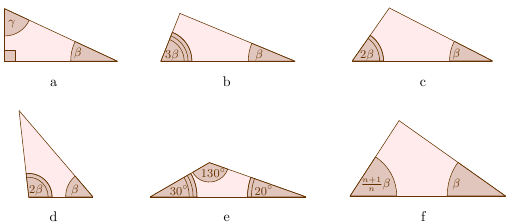
Среди этих примеров есть и нетривиальные.
Всю эту ерунду я откопал в статье
Mikhail Skopenkov
Packing a cake into a box |
|
|
| номер сообщения: 49-2-2965 |
|
|
|
|
MikhailK:
Если минимизировать число кусков, то ответ вот такой
 |
Двух прямолинейных разрезов всегда хватает.
А я был знаком с братом автора статьи... |
|
|
| номер сообщения: 49-2-2966 |
|
|
|
|
| iourique: Двух прямолинейных разрезов всегда хватает. |
А как? У меня вот так сходу не получилось.
iourique:
А я был знаком с братом автора статьи... |
Тесен мир  |
|
|
| номер сообщения: 49-2-2967 |
|
|
|
|
MikhailK: | iourique: Двух прямолинейных разрезов всегда хватает. |
А как? У меня вот так сходу не получилось.
|
Соединить основание высоты на одной стороне с серединами двух других - все три полученных куска обладают осевой симметрией. |
|
|
| номер сообщения: 49-2-2968 |
|
|
|
|
| iourique: Соединить основание высоты на одной стороне с серединами двух других - все три полученных куска обладают осевой симметрией. |
Стоп, я ведь тоже делал это построение. Я только зачем-то и высоту считал за разрез, а этого можно было и не делать.

Здорово. |
|
|
| номер сообщения: 49-2-2969 |
|
|
|
|
"ВРЕМЯ новостей" 23.03.2010
Теория других чисел Дарья Луганская
Российский математик может отказаться от премиального миллиона
Известный равнодушным отношением к регалиям и чекам на суммы с шестью нулями, математик Григорий Перельман удостоился «премии тысячелетия». Математический институт Клея (Кембридж, США) присудил ему эту награду за решение загадки, казавшейся неразрешимой, -- в 2002 году г-н Перельман доказал гипотезу Пуанкаре. На церемонии награждения 46-летнего ученого, живущего в скромной двухкомнатной квартире в спальном районе Санкт-Петербурга, ждут не только лавры, но и 1 млн долл. Заокеанские ученые говорят, что российский математик думает над тем, чтобы принять премию. Но коллеги петербургского самородка уверены: Григорий Перельман не изменит своим принципам. Четыре года назад он непринужденно отказался от медали Филдса, по статусу равной Нобелевской премии.
«Я уже связывался с господином Перельманом, сообщил ему о присуждении нашей премии, и он сказал, что польщен этим», -- сказал ИТАР-ТАСС президент института Клэя Джеймс Карлсон. Он приводит слова самого Перельмана: математик заверил американского коллегу, что «подумает, над тем, чтобы принять премию». Но это заверение не вселило надежды Джеймсу Карлсону. «Мы намерены 8 и 9 июня этого года провести в Париже конференцию, на которой будет отмечаться обретение доказательства теории Пуанкаре, и там хотели бы вручить господину Перельману премию, но я думаю, что он вряд ли приедет туда», -- заметил он. Вторят американскому ученому и бывшие коллеги Перельмана. «Не думаю, что он вдруг возьмет и решит принять премию в один миллион долларов от Математического института Клея», -- заявил директор Математического института им В.А. Стеклова РАН Сергей Кисляков. Сам Перельман никаких комментариев традиционно не дает. Представители СМИ получили «от ворот поворот» в его квартире в Купчино, его телефон не отвечает, электронные письма на его адрес остаются безответными.
В этой истории примечательно и то, что институту Клея ради награждения российского математика пришлось нарушить собственные правила. По ним получить «премию тысячелетия» может только автор, опубликовавший свои работы в рецензируемых журналах. А доказательство Григория Перельмана было вывешено во Всемирной сети. Как напоминает Lenta.ru, его работа так и осталась набором из трех статей за подписью Grisha Perelman на сайте arXiv.org.
В 2002--2003 годах российский ученый просто разместил результаты восьмилетнего труда в этом сетевом архиве. Детали решения он не разъяснял. Но и в общем виде разгадка одного из «математических чудес света», над которым сотню лет ломали головы ученые, стала сенсацией в среде специалистов. Загадочная гипотеза, выдвинутая Анри Пуанкаре в 1904 году, -- самая знаменитая задача топологии. Ее формулировка для непосвященных едва ли понятна: «каждая односвязная трехмерная поверхность гомеоморфна трехмерной сфере». В упрощенном для обывателей виде она выглядит так: «Если вы опояшете одной резиновой лентой апельсин, а другой -- бублик с дыркой и сожмете их, ленты будут вести себя по-разному. Лента на апельсине будет сжиматься, не разрываясь и не соскакивая с поверхности. Лента на бублике либо разорвется сама, либо разорвет сам бублик». Ученые полагают, что разгадка гипотезы позволит сделать серьезный шаг в математическом описании сложных объектов, даст новый толчок развитию компьютерной топологии и может привести к открытию нового направления в геометрии.
В течение двух лет после публикации математики проверяли неопровержимость доказательства. Только при этом условии институт Клея обязался поощрить гения обещанной за решение загадки Пуанкаре медалью Филдса. Но доскональная проверка не лишила Перельмана звания первооткрывателя. Серьезных ошибок в его работах так и не нашли. А это означало, что никаких преград для награждения его премией, имеющей статус Нобелевской и размер 1 млн долл., больше не существовало. Но российский ученый в 2006 году не просто не принял высокую награду, но даже не приехал на вручение, не удостоив математическое сообщество никакими объяснениями. Правда, для коллег жест Перельмана вряд ли был неожиданностью. Математик уже был известен тем, что не обращает внимания на награды. Петербургский ученый отказался от Европейской математической премии, да и медаль Филдса уже один раз проигнорировал в 1996 году.
Именно репутация вечного отказника в математическом сообществе и дает основание коллегам ученого предполагать, что г-н Перельман не изменит свою позицию. Сам факт присуждения ему «премии тысячелетия» свидетельствует о том, что доказательство гипотезы Пуанкаре, выполненное российским математиком, официально признано верным. А в общественном сознании Григорий Перельман пока так и остается лишенным тщеславия гением от математики. |
|
|
| номер сообщения: 49-2-2986 |
|
|
|
|
LatchezarS:
| Дарья Луганская: Лента на бублике либо разорвется сама, либо разорвет сам бублик. |
|
Ага, капля никотина убивает лошадь, а хомячка разрывает на куски.... Ну и премию Клея с Филдсовской медалью можно было бы не путать. |
|
|
| номер сообщения: 49-2-2987 |
|
|
|
|
Задачка в тему:
В стену вбито два гвоздя. Можно ли повесить на них веревочную петлю так, чтобы она падала, если вытащить из стены любой из гвоздей? |
|
|
| номер сообщения: 49-2-2988 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2026 гг. |
|
|
|