|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
Кстати, а нельзя ли довольно точно оценить число легальных позиций в духе метода Монте-Карло. Выбираем случайным образом произвольную позицию и проверяем ее на легальность. Перебрав достаточное количество позиций (хватит мощностей?) можно будет получить долю легальных позиций. Число же всех позиций вроде можно довольно просто вычислить.
PS Похоже, что в моем подходе нужно считать доли легальных позиций для каждого набора фигур отдельно и только потом вычислять полное число легальных позиций. |
|
|
| номер сообщения: 49-2-2687 |
|
|
|
|
| MikhailK: PS Похоже, что в моем подходе нужно считать доли легальных позиций для каждого набора фигур отдельно и только потом вычислять полное число легальных позиций. |
Мне тоже казалось, что в этом основная загвоздка, учитывая, что разных наборов - 75 миллионов :)
Еще одна проблема в том, что даже одну позицию проверить на легальность не так-то просто. Легальна ли, например, такая позиция?
|
|
|
| номер сообщения: 49-2-2688 |
|
|
|
|
Число позиций и число партий вещь разная. Не только потому, что возможны повторы позиций (это сильно увеличивает сумму), но и потому, что должны быть исключены все нелегальные положения.
Последние довольно трудно посчитать (скажем, как оценить кол-во позиций, где король под шахом, а право хода принадлежит противнику?) |
|
|
| номер сообщения: 49-2-2689 |
|
|
|
|
iourique: | MikhailK: PS Похоже, что в моем подходе нужно считать доли легальных позиций для каждого набора фигур отдельно и только потом вычислять полное число легальных позиций. |
Мне тоже казалось, что в этом основная загвоздка, учитывая, что разных наборов - 75 миллионов :)
Еще одна проблема в том, что даже одну позицию проверить на легальность не так-то просто. Легальна ли, например, такая позиция?
|
Я бы различал легальные позиции и позиции достижимые из начальной расстановки. Насколько я понимаю, число достижимых позиций посчитать гораздо сложнее. Я под легальными позициями понимал не только достижимые, а все, которые не противоречат правилам шахмат (оба короля не под шахом, нет тройных шахов, и т. д.).
Что касается большого количества разных наборов, то мне кажется, что здесь проблемы не возникнет. Во-первых, эта задача легко распараллеливается, а во-вторых, многие наборы можно будет не обсчитывать из-за малого числа всех расстановок в них. |
|
|
| номер сообщения: 49-2-2690 |
|
|
|
|
azur: Число позиций и число партий вещь разная. Не только потому, что возможны повторы позиций (это сильно увеличивает сумму), но и потому, что должны быть исключены все нелегальные положения.
Последние довольно трудно посчитать (скажем, как оценить кол-во позиций, где король под шахом, а право хода принадлежит противнику?) |
azur, я тремя постами выше приводил оценку, по которой число партий - экспонента от числа позиций, так что да, это сильно разные вещи, мы их просто обсуждаем вперемешку :) Можно еще различать позиции и диаграммы - в этом случае в понятие "позиция" входят такие вещи, как право на рокировку, возможность взятия на проходе и очередь хода. Об этом Roger писал.
Что касается подсчета именно легальных позиций, то мне это представляется довольно безнадежной задачей: грубые оценки не будут отличать число легальных позиций от общего числа позиций (после того, как мы позаботимся о том, чтобы на доске были два короля, не больше 30 других фигур, не больше 8 пешек с каждой стороны, и прочих простых для учета вещах); а для точных оценок придется придумать очень хороший алгоритм определения легальности. |
|
|
| номер сообщения: 49-2-2691 |
|
|
|
|
iourique: Легальна ли, например, такая позиция?
|
Даже такая легальна:
| iourique: p.p.s. Мы, разумеется, не пользуемся правилом 50 ходов. |
Тогда даже число партий, начинающихся и заканчивающихся в одной и той же начальной расстановке, будет бесконечным .. (если при этом и правилом троекратного повтора не пользоваться)  |
|
|
| номер сообщения: 49-2-2692 |
|
|
|
|
MikhailK:
Я бы различал легальные позиции и позиции достижимые из начальной расстановки.... Я под легальными позициями понимал не только достижимые, а все, которые не противоречат правилам шахмат (оба короля не под шахом, нет тройных шахов, и т. д.). |
Мне это кажется немного искусственным. Легальна ли позиция, в которой у белых 10 ферзей? И мне почему-то не хочется считать легальной такую позицию:
| Что касается большого количества разных наборов, то мне кажется, что здесь проблемы не возникнет. Во-первых, эта задача легко распараллеливается, а во-вторых, многие наборы можно будет не обсчитывать из-за малого числа всех расстановок в них. |
Во второе я не очень верю, а первое, конечно, правда - можно попробовать. |
|
|
| номер сообщения: 49-2-2693 |
|
|
|
|
azur: Даже такая легальна:
|
И впрямь.
| iourique: p.p.s. Мы, разумеется, не пользуемся правилом 50 ходов. |
Тогда даже число партий, начинающихся и заканчивающихся в одной и той же начальной расстановке, будет бесконечным .. (если при этом и правилом троекратного повтора не пользоваться)  |
Э нет. Троекратное повторение позиции. |
|
|
| номер сообщения: 49-2-2694 |
|
|
|
|
iourique: | iourique: p.p.s. Мы, разумеется, не пользуемся правилом 50 ходов. |
Тогда даже число партий, начинающихся и заканчивающихся в одной и той же начальной расстановке, будет бесконечным .. (если при этом и правилом троекратного повтора не пользоваться)  |
Э нет. Троекратное повторение позиции. |
А сможем посчитать кол-во партий, приведших к начальной расстановке фигур при таких условиях? (3-кратный повтор=ничья, правило 50 ходов не действует) |
|
|
| номер сообщения: 49-2-2695 |
|
|
|
|
| azur: А сможем посчитать кол-во партий, приведших к начальной расстановке фигур при таких условиях? (3-кратный повтор=ничья, правило 50 ходов не действует) |
PS. Повторы желательно учитывать по правилам ФИДЕ, т.е. при повторении позиции также должно повторяться наличие или отсутствие права на конкретную рокировку. |
|
|
| номер сообщения: 49-2-2696 |
|
|
|
|
В результате некоторых размышлений о числе легальных позиций я пришёл вот к такой задаче. Рассмотрим позицию
Ясно, что она ничейна. Могут ли белые и черные пререйти четырехферзевый эндшпиль так, чтобы ничейность позиции сохранялась при каждом ходе?
К такой задаче меня привели следующие мысли. Мне кажется, что большинство легальных позиций являются неинтересными (нелогичными), т.е. не могут быть получены из начальной расстановки при идеальной игре сторон.
Например, рассмотрим какую-нибудь легальную позицию с пешками. Оставим теперь фигуры на своих местах, а пешки начнем заменять на различные легкие и тяжелые фигуры. Естественно, что часть полученных таким образом расстановок не будут легальными, но, мне кажется, что их доля не будет уж очень большой. Если это так, то выходит, что основная масса легальных расстанок является беспешечными и в реальных партиях встречается исключительно редко. Кроме того, у меня есть ощущение, что при правильной игре сторон подобные беспешечные расстановки практически не будут появляться.
Для доказательства этого я решил начать с простейшей задачи, которую сформулировал выше. Я сделал несколько попыток перейти там в четырехферзевый эндшпиль (с Налимовскими базами), но у меня ничего не вышло. |
|
|
| номер сообщения: 49-2-2697 |
|
|
|
|
MikhailK: В результате некоторых размышлений о числе легальных позиций я пришёл вот к такой задаче. Рассмотрим позицию
Ясно, что она ничейна. Могут ли белые и черные пререйти четырехферзевый эндшпиль так, чтобы ничейность позиции сохранялась при каждом ходе?
|
Без проблем. |
|
|
| номер сообщения: 49-2-2698 |
|
|
|
|
Вот, например, более-менее правдоподобное развитие событий:
1.f4 c5 2-5.f8Q c1Q 6.Qf6 b5 7.g4 b4 8.g5 b3 9.g6 b2 10.Qf7+ Ka8 11.g7 b1Q 12.g8Q+ Qb8+ и т.д. |
|
|
| номер сообщения: 49-2-2699 |
|
|
|
|
azur: | azur: А сможем посчитать кол-во партий, приведших к начальной расстановке фигур при таких условиях? (3-кратный повтор=ничья, правило 50 ходов не действует) |
PS. Повторы желательно учитывать по правилам ФИДЕ, т.е. при повторении позиции также должно повторяться наличие или отсутствие права на конкретную рокировку. |
По-моему, неподъемно. Даже если запретить ходить ладьями и учесть, что белым коням нельзя попадать на d6 и f6, а черным соответственно на d3 и f3 (их там придется съесть), то все равно возможных позиций больше миллиона. При этом в некоторых из них довольно много ходов, а в некоторых - не очень. Есть даже невозможные позиции:
Как при этом считать число циклических маршрутов, я не знаю. |
|
|
| номер сообщения: 49-2-2700 |
|
|
|
|
iourique: azur: | azur: А сможем посчитать кол-во партий, приведших к начальной расстановке фигур при таких условиях? (3-кратный повтор=ничья, правило 50 ходов не действует) |
PS. Повторы желательно учитывать по правилам ФИДЕ, т.е. при повторении позиции также должно повторяться наличие или отсутствие права на конкретную рокировку. |
По-моему, неподъемно. |
Нда .. как минимум - непросто. Даже если совсем уж упростить, запретить ходить ладьями и уже первый повтор считать ничьей ..
iourique: Есть даже невозможные позиции:
|
Вторая симметрична:
Других вроде бы нет .. |
|
|
| номер сообщения: 49-2-2701 |
|
|
|
|
azur: Вторая симметрична:
|
А вот и нет! Ваша - возможная, так как в ней ход черных. Правда, она тупиковая - вернуться в начальную не получится. |
|
|
| номер сообщения: 49-2-2702 |
|
|
|
|
iourique: azur: Вторая симметрична:
|
А вот и нет! Ваша - возможная, так как в ней ход черных. Правда, она тупиковая - вернуться в начальную не получится. |
Да и в предыдущей ход черных. Она невозможная именно в том смысле, что из нее нельзя достичь начальной расстановки - в будущем у этой позиции последует нарушение условия, а для предыдущей ясно, что в ее прошлом уже было нарушение .. |
|
|
| номер сообщения: 49-2-2703 |
|
|
|
|
небольшая выдержка из забавного текста
Исследователей заинтересовал вопрос, который уже достаточно давно мучает спортсменов-гребцов. Предположим, мы рассадили их в длинную гребную лодку и дали каждому по веслу. Спортсмен может грести либо с одного борта лодки, либо с другого. При этом, разумеется, каждый его гребок сообщает лодке ускорение, поперечное направлению движения. Возникает вопрос, как рассадить людей так, чтобы в результате лодка в перпендикулярном направлении не колебалась. Как оказалось, это равносильно следующей задаче: в наборе подряд идущих целых чисел 1, 2, ..., N необходимо расставить знаки так, чтобы сумма чисел оказалась равна нулю.
В рамках исследования, помимо теоретических результатов, касающихся данной задачи (например, оказывается, это можно сделать только в том случае, если N кратно четырем, то есть 4, 8, 16 и так далее) исследователи сделали неожиданное практическое открытие - им удалось обнаружить рассадку восьмерки (лодки, в которой восемь гребцов и рулевой), которая ранее никому не была известна.
Возможные рассадки спортсменов в лодке. Пункт a) был ранее неизвестен, b) - немецкая рассадка, с) и d) получаются склейкой одинаковых и зеркально отраженных итальянских четверок соответственно. Им соответствуют решения:
a) 1 + 2 - 3 - 4 - 5 - 6 + 7 + 8 = 0
b) 1 - 2 + 3 - 4 - 5 + 6 - 7 + 8 = 0
c) 1 - 2 - 3 + 4 + 5 - 6 - 7 + 8 = 0
d) 1 - 2 - 3 + 4 - 5 + 6 + 7 - 8 = 0 |
Подозреваю, что рассадка a) была и ранее известна, но ею никто не пользовался по каким-то спортивным причинам (подряд 4 гребца гребут с одного борта). |
|
|
| номер сообщения: 49-2-2733 |
|
|
|
|
Прошу прощения за прошлогоднюю новость. 31 декабря Фабрис Беллар установил новый мировой рекорд по точности вычисления числа пи. Вычисления проводились по формуле Чудновского, а проверка вычислений по формуле Беллара.
Новость сама по себе не очень интересная, но пройдя по ссылке я обнаружил новую для себя формулу для числа пи
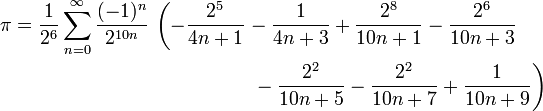
Кстати, тут можно посмотреть элементарный вывод этой формулы.
В связи с подобными новостями обычно приговаривают, что цифры 0-9 распределены равновероятно в десятичном разложении числа пи. Интересно, а является ли десятичная запись числа пи хорошим источником случайных чисел? Хорошо ли себя там ведут разные корреляторы или есть аномалии? |
|
|
| номер сообщения: 49-2-2736 |
|
|
|
|
| В блоге Тима Гауэрса обсуждают очень забавную задачку - кстати, нерешенную. Я уже неделю насилую рабочий компьютер... |
|
|
| номер сообщения: 49-2-2741 |
|
|
|
|
| iourique: В блоге Тима Гауэрса обсуждают очень забавную задачку - кстати, нерешенную. Я уже неделю насилую рабочий компьютер... |
Почитал, забавно, но за нерешенные математические(!) задачи я не берусь. 
А что там в блоге такая огромная толпа делает? Там есть какой-то распределённый подход к этой проблеме? |
|
|
| номер сообщения: 49-2-2742 |
|
|
|
|
| MikhailK: А что там в блоге такая огромная толпа делает? Там есть какой-то распределённый подход к этой проблеме? |
По-моему, нет. Идея polymath projects в том, что много народу что-то делает вместе, любое разделение обязанностей возникает спонтанно, по интересам. Эксперимент довольно удачный - вот предыдущий результат. |
|
|
| номер сообщения: 49-2-2743 |
|
|
|
|
| номер сообщения: 49-2-2744 |
|
|
|
|
Лента зажгла на эту тему:
| Подобные вычисления имеют не только прикладное значение. Так, в настоящее время с Пи связано множество нерешенных задач. Например, известно, что Пи и e (основание экспоненты) являются трансцендентными числами, то есть не являются корнями никакого многочлена с целыми коэффициентами. При этом, однако, является ли сумма этих двух фундаментальных констант трансцендентным числом или нет - неизвестно до сих пор. |
Любопытно, какое они видят прикладное значение в знании триллионного знака пи? Еще любопытнее, как это может кому-нибудь помочь узнать, трансцендентно ли пи+е? |
|
|
| номер сообщения: 49-2-2763 |
|
|
|
|
| iourique: Любопытно, какое они видят прикладное значение в знании триллионного знака пи? Еще любопытнее, как это может кому-нибудь помочь узнать, трансцендентно ли пи+е? |
Если пи+е окажется алгебраическим числом, то уверен, что весь математический мир будет потрясен, если кто-нибудь сможет предъявить соответствующий полином с целыми коэффициентами, корнем которого является пи+е. |
|
|
| номер сообщения: 49-2-2764 |
|
|
|
|
Очень понравилась простенькая задачка, рассказанная drowsy у Кванта:
На плоскости внутри прямоугольника вырезали прямоугольную дырку. Пользуясь только линейкой поделить эту фигуру прямой линией на две части равной площади. |
|
|
| номер сообщения: 49-2-2767 |
|
|
|
|
| Задача действительно забавная. Вот только что-то я её решил неправдоподобно бысто. |
|
|
| номер сообщения: 49-2-2768 |
|
|
|
|
| Провести прямую через центры прямоугольников? |
|
|
| номер сообщения: 49-2-2769 |
|
|
|
|
| Roger: Провести прямую через центры прямоугольников? |
У меня аналогичное решение. |
|
|
| номер сообщения: 49-2-2770 |
|
|
|
|
MikhailK: | iourique: Любопытно, какое они видят прикладное значение в знании триллионного знака пи? Еще любопытнее, как это может кому-нибудь помочь узнать, трансцендентно ли пи+е? |
Если пи+е окажется алгебраическим числом, то уверен, что весь математический мир будет потрясен, если кто-нибудь сможет предъявить соответствующий полином с целыми коэффициентами, корнем которого является пи+е. |
Заглянул сюда после долгого перерыва и вздрогнул. Потому что мне недавно пришла в голову (не знаю, откуда пришла) такая мысль: какая разница, является ли какое-то число рациональным, иррациональным или алгебраическим? Какая за этим стоит философия? Математику можно разделить на ту, для которой это важно и на ту, для которой это не важно?..
ЗЫ Мой первый начальник, человек очень умный и хороший, к тому же известнейший специалист в области выч. техники, любил говаривать: "Что больше: ежды пи или пижды е?"... |
|
|
| номер сообщения: 49-2-2771 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2025 гг. |
|
|
|