|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
MikhailK: iourique:
Здесь используется обозначение
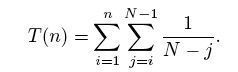
|
А почему индекс i не встречается под знаком суммы? |
Встречается. Аккурат под знаком суммы  . .
Интересно, а как твое общее решение можно получить в рамках моего подхода? |
А черт его знает. Видимо, надо более аккуратно разбираться с коэффициентами C_m^k. |
|
|
| номер сообщения: 49-2-1723 |
|
|
|
|
iourique: MikhailK: iourique:
Здесь используется обозначение
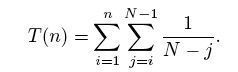
|
А почему индекс i не встречается под знаком суммы? |
Встречается. Аккурат под знаком суммы  . .
|
Действительно. 
iourique:
Интересно, а как твое общее решение можно получить в рамках моего подхода? |
А черт его знает. Видимо, надо более аккуратно разбираться с коэффициентами C_m^k. |
Да, там вроде все просто. Похоже, что достаточно минимальных изменений в вычислениях. Попробую посчитать на днях. |
|
|
| номер сообщения: 49-2-1724 |
|
|
|
|
Кстати, у ответа есть интерпретация через диаграммы Юнга. Скажем, начальная расстановка для 5 шариков - диаграмма Юнга с одним горизонтальным рядом длины 5. Конечная - столбец высоты 5. Пропихнуть клетку на один уровень вниз стоит денег - причем, чем ниже уровень, тем дороже. Переход с первого уровня на второй - 1 рубль, со второго на третий - 4/3 рубля, с третьего на четвертый - 4/2 рубля, а с четвертого на пятый - 4 рубля. Нам надо оплатить переход одной клетки с первого уровня на пятый (4/4+4/3+4/2+4/1), другой - с первого на четвертый (4/4+4/3+4/2), третьей - с первого на третий (4/4+4/3), и четвертой - с первого на второй (4/4). Общая цена - 16 рублей. Вычисление работает и для других диаграмм.
Бонусная задача. Из равномерного распределения на отрезке [0,1] независимо выбраны 4 точки. Они разбивают отрезок [0,1] на 5 отрезков. Пусть l_1 - длина самого короткого из этих отрезков, l_2 - второго по длине, и т.д. (l_5 - длина самого длинного). Чему равно матожидание l_i? |
|
|
| номер сообщения: 49-2-1726 |
|
|
|
|
| iourique: Кстати, у ответа есть интерпретация через диаграммы Юнга.... |
У меня есть друзья, кототые только тем и занимаются, что рисуют диаграммы Юнга. Как бы я к ним не зашел, все листы покрыты паровозиками разной длины и конфигурации.
iourique:
Бонусная задача. Из равномерного распределения на отрезке [0,1] независимо выбраны 4 точки. Они разбивают отрезок [0,1] на 5 отрезков. Пусть l_1 - длина самого короткого из этих отрезков, l_2 - второго по длине, и т.д. (l_5 - длина самого длинного). Чему равно матожидание l_i? |
iourique, знаете анекдот про блох?
| К экзамену по биологии студент выучил только одну тему - "Блохи". В его билете три вопроса: "Млекопитающие", "Птицы" и "Рыбы". Студент отвечает на первый вопрос: "Млекопитающие покрыты шерстью. В шерсти водятся блохи"… и далее очень подробно про блох. Преподаватель говорит: "Хорошо. Теперь второй вопрос - птицы". Студент: "Птицы покрыты перьями. Это все равно, что шерсть у млекопитающих. А, как известно, в шерсти водятся блохи…" И далее опять про блох. "Хорошо, третий вопрос". "Третий вопрос - рыбы. У рыб шерсти нет. Но если бы была, то в ней бы водились блохи…" |
Вот так я учил в свое время теорию вероятности. Если задачка по терверу быстро сводилась к блохам интегралам, то хорошо, а иначе... |
|
|
| номер сообщения: 49-2-1728 |
|
|
|
|
iourique, что скажете о такой задаче.
Вдоль оси x могут двигаться без трения два шарика с массами m и M. Слева от шариков поставлена абсолютно упругая стенка, от которой шарики отскакивают без потери энергии (ясно, что со стенкой будет сталкиваться только шарик с массой m). Столкновения шариков между собой также считаются упругими.

Пусть в начальный момент времени шарик с массой M движется по направлению с стенке, а шарик с массой m неподвижен. Тогда после нескольких столкновений шариков между собой и со стенкой шарик с массой M будет лететь от стенки, а ещё через несколько столкновений шарик с массой M будет иметь скорость больше, чем шарик с массой m и столкновения в системе прекратятся. Другими словами, суммарное число столкновений (со стенкой и шариков между собой) в системе будет конечным.
Вопрос. Найти суммарное число столкновений в системе. Чтобы прочувствовать фееричность задачи, найдите суммарное число столкновений в системе для отношения масс шариков равным m/M=10^(-2*q), где q - целое положительное число. |
|
|
| номер сообщения: 49-2-1730 |
|
|
|
|
MikhailK: iourique, что скажете о такой задаче.
Вдоль оси x могут двигаться без трения два шарика с массами m и M. Слева от шариков поставлена абсолютно упругая стенка, от которой шарики отскакивают без потери энергии (ясно, что со стенкой будет сталкиваться только шарик с массой m). Столкновения шариков между собой также считаются упругими.

Пусть в начальный момент времени шарик с массой M движется по направлению с стенке, а шарик с массой m неподвижен. Тогда после нескольких столкновений шариков между собой и со стенкой шарик с массой M будет лететь от стенки, а ещё через несколько столкновений шарик с массой M будет иметь скорость больше, чем шарик с массой m и столкновения в системе прекратятся. Другими словами, суммарное число столкновений (со стенкой и шариков между собой) в системе будет конечным.
Вопрос. Найти суммарное число столкновений в системе. Чтобы прочувствовать фееричность задачи, найдите суммарное число столкновений в системе для отношения масс шариков равным m/M=10^(-2*q), где q - целое положительное число. |
Отличная задача. Еще не решил, но уже, кажется, знаю ответ: приближения пи. Круто.
UPD. Более не менее дорешал. Ответ: 2*pi/а, где а = arcsin(2 sqrt(M m)/(M+m)). Округлить надо, конечно, и, может один добавить. При приведенном соотношении масс получается pi*10^q. |
|
|
| номер сообщения: 49-2-1731 |
|
|
|
|
MikhailK:
Вот так я учил в свое время теорию вероятности. Если задачка по терверу быстро сводилась к блохам интегралам, то хорошо, а иначе... |
Эта сводится. |
|
|
| номер сообщения: 49-2-1732 |
|
|
|
|
MikhailK: iourique, что скажете о такой задаче.
Вдоль оси x могут двигаться без трения два шарика с массами m и M. Слева от шариков поставлена абсолютно упругая стенка, от которой шарики отскакивают без потери энергии (ясно, что со стенкой будет сталкиваться только шарик с массой m). Столкновения шариков между собой также считаются упругими.

Пусть в начальный момент времени шарик с массой M движется по направлению с стенке, а шарик с массой m неподвижен. Тогда после нескольких столкновений шариков между собой и со стенкой шарик с массой M будет лететь от стенки, а ещё через несколько столкновений шарик с массой M будет иметь скорость больше, чем шарик с массой m и столкновения в системе прекратятся. Другими словами, суммарное число столкновений (со стенкой и шариков между собой) в системе будет конечным.
Вопрос. Найти суммарное число столкновений в системе. Чтобы прочувствовать фееричность задачи, найдите суммарное число столкновений в системе для отношения масс шариков равным m/M=10^(-2*q), где q - целое положительное число. |
При столкновении шариков и последующем столкновении маленького шарика со стенкой скорости пересчитываются по формуле
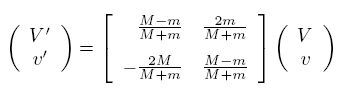
Столкновения прекратятся, когда

где
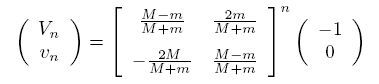
Собственные значения матрицы равны

Соответствующие собственные вектора -

Отсюда,

И значит, необходимо, чтобы выполнялось
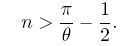
Суммарное же число столкновений вдвое больше, чем n (возможно 2n-1, в зависимости от того, перепрыгнули мы через пи или нет). |
|
|
| номер сообщения: 49-2-1734 |
|
|
|
|
LatchezarS: Монгольская задача :
В шахматном турнире участвовало 10 шахматистов.
Все участники турнира набрали разлчное число очков.
Занявщие первое и второе места не проиграли ни одной встречи и набрали на 10 очков больше ,
чем занявший третье место.
Шахматист , занявший четвертое место , набрал столько же очков , сколько набрали вместе
занявшие четь/ре последних места в таблице результатов.
Сколько очков нарали шахматисть/ , заняшхие с первого по шестое место? |
Где-то я это уже читал. Хотя задача Grigoriy была немного по другому сформулирована |
|
|
| номер сообщения: 49-2-1737 |
|
|
|
|
iourique:
Суммарное же число столкновений вдвое больше, чем n (возможно 2n-1, в зависимости от того, перепрыгнули мы через пи или нет). |
ага.
Я тут ещё немного покрутил задачу с шариками. На днях напишу. Как выяснилось, один знакомый алгебраист таки клюнул на задачку и пытается найти в ней суть. В пятницу мучал меня диграммами Юнга. |
|
|
| номер сообщения: 49-2-1738 |
|
|
|
|
iourique: Мое решение выглядит так: пусть A(n_1, n_2,..,n_N)- число шагов, требуемое для перекраски n_1 шариков цвета 1, n_2 шариков цвета 2, и т.д. в один цвет. Тогда
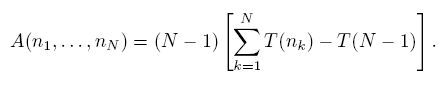
Здесь используется обозначение
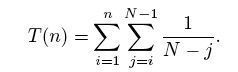
Формула угадана наблюдением за случаем 6 шариков  . Доказательство очень просто - проверить, что А удовлетворяет системе линейных уравнений. В частности, А(1,1,...,1)=(N-1)*(N-1). . Доказательство очень просто - проверить, что А удовлетворяет системе линейных уравнений. В частности, А(1,1,...,1)=(N-1)*(N-1). |
А у меня получился вот такой ответ

В этой формуле s_i - число шаров i-ого цвета в начальный момент. Мне пока совсем не очевидно, что наши формулы совпадают.
PS iourique, не является ли задачка с шариками в мешке некоторым обобщением задачи об урне Полиа. |
|
|
| номер сообщения: 49-2-1739 |
|
|
|
|

На берегу Байкаля вь/строились в ряд пять палаток окрашень/е в различнь/х цветов.
Обитатели палаток прибь/ли из пяти разнь/х стран , их вкусь/ разходятся решительно во всем.
Каждь/й из них имеет любимую игру - причем у всех разнь/е.
Все пятеро - заядль/е курильщики ,но то , что курит один,ни за какие блага не станет курить другой.
Любой отдает предпочтение одному из пяти напитков , не любимому более никем другим.
1.В красной палатке живет русский.
2.У англичанина ,согласно британским традициям - футбольнь/й мяч.
3.Обитатель зеленой палатки пьет кофе.
4.Француз пьет шампаньское и поддерживает дружеские отношения с обитателем синей палатки.
5.Зеленая палатка расположена правее белой.
6.У того ,кто курит сигареть/"Кент" - игра "Го".
7.Обитатель серой палатки любит вь/куриват сигару,сидя у входа в палатку.
8.У обитателя средней палатке - недавно вскипело молоко.
9.Болгарин живет слева ,в первой палатки.
10.Человек , только что набивший трубку ,живет слева от того , кто привез с собой карть/.
11.Слева от любителя сигар разположился владелец шашечного комплекта.
12.Один из обитателей палаток заявил:
-Я согласен,что курит сигареть/ "Лорд" довольно накладно,но зато я пью лишь газированную воду.
13.Если послушат поляка,то нет ничего лучше сигарет "Ароматнь/е".
14.Болгарин живет по соседству с синей палаткой.
Определите НАЦИОНАЛЬНОСТЬ ШАХМАТИСТА,и установите В КАКОЙ ИЗ ПАЛАТОК слева от его палатки ЖИВЕТ
ЛЮБИТЕЛЬ ВОДКИ.
п.п. Логическая задача особой трудности!
Рассматриваемая задача отличается тем , что в ней число множесв , между злементами которь/х
необходимо установить взаимно-однозначное соответствие , равно не двум, не трем и даже не четь/рем,
а шести (национальность; напиток; что курит; цвет палатки; номер палатки; игра).
Позтому задачу можно считать шестмерной логической задачей.
Решение " под гребенку" не получится. |
|
|
| номер сообщения: 49-2-1741 |
|
|
|
|
MikhailK: iourique: Мое решение выглядит так: пусть A(n_1, n_2,..,n_N)- число шагов, требуемое для перекраски n_1 шариков цвета 1, n_2 шариков цвета 2, и т.д. в один цвет. Тогда
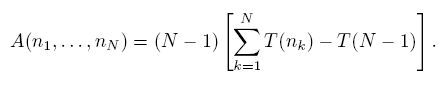
Здесь используется обозначение
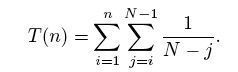
Формула угадана наблюдением за случаем 6 шариков  . Доказательство очень просто - проверить, что А удовлетворяет системе линейных уравнений. В частности, А(1,1,...,1)=(N-1)*(N-1). . Доказательство очень просто - проверить, что А удовлетворяет системе линейных уравнений. В частности, А(1,1,...,1)=(N-1)*(N-1). |
А у меня получился вот такой ответ

В этой формуле s_i - число шаров i-ого цвета в начальный момент. Мне пока совсем не очевидно, что наши формулы совпадают. |
Идентичность формул следует из равенства

Его несложно доказать по индукции, но комбинаторный смысл от меня ускользает... |
|
|
| номер сообщения: 49-2-1744 |
|
|
|
|
Grigoriy: Ну и ещё одна (знакомая тут многим :-) ) задача на ясное мышление.
Есть небоскрёб в 100 этажей. Имеем 2 абсолютно одинаковых стеклянных шарика. За какое наименьшее число бросаний можно гарантированно определить, при бросании с какого наинизшего этажа шарик разбивается. |
azur: -В свое время в одном из параллельных миров писал об обобщении на случай многих попыток и шариков ...
АЗУР,не знаю как надо поставит таблицу,так что НАЖМИТЕ "ЦИТИОВАТЬ" и читайте. Л.Станчев
Общая задача:
Есть небоскрёб в L этажей. Имеем n абсолютно одинаковых стеклянных шарика. За какое наименьшее g число бросаний можно гарантированно определить, при бросании с какого наинизшего этажа шарик разбивается.
Вот мое решение :
Анализ
После любого i-ого сбрасивания возможно только 2 результата
а) (n - 1) к-во шариков сократилос на единицу , (g - 1) к-во бросков сократилос на единицу
b) n к-во шариков не изменилос , (g - 1) к-во бросков сократилос на единицу
ЗНАЯ: ( По ходу заполнения таблиць/ зто легко)
La -число зтажей обследуемь/е при (n)шарика и (g-1)бросков,
Lв -число зтажей обследуемь/е при (n-1)шариков и (g-1) бросков.
*Единицу добавляем , чтобь/ взят на учет и зтаж с которого бросили шарик
НАХОДИМ Lх = La + Lв + 1
Следовательно,
СРАЗУ И ОЧЕНЬ ЛЕГКО*, начиная с нижнего левого угла, ЗАПОЛНЯЕМ ТАБЛИЦУ:
Там где пересекаются (ni) и (gii) запишем число Li;gii - зтажи небоскреба которь/е
гарантировано можем обследоват имея ni шарика за gii броска.
n количество шариков
. 1 2 5 11 23 47 95 191 383 767 1535 3071 6143 12287
. . . . . . . . . . . . . . .
. . La Lх . . . . . . . . . . .
. . Lв . . . . . . . . . . . .
9 1 2 5 11 23 47 95 191 383 767 1533 3048 5997 11610
8 1 2 5 11 23 47 95 191 383 765 1514 2948 5612 10400
7 1 2 5 11 23 47 95 191 381 748 1433 2663 4787 8321
6 1 2 5 11 23 47 95 189 366 684 1229 2123 3533 5681
5 1 2 5 11 23 47 93 176 317 544 893 1409 2147 3173
4 1 2 5 11 23 45 82 140 226 348 515 737 1025 1391
3 1 2 5 11 21 36 57 85 121 166 221 287 365 456
2 1 2 5 9 14 20 27 35 44 54 65 77 90 104
1 1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13 14 g
количество
бросков
Как вь/числит любое табличное L ?
Любое Lх = Lа + Lв + 1
Начинаем с нижнего левого угла L = 2 + 2 +1 = 5 ; L' = L + 3 + 1 = 9 ; L'' = L + L + 1 = 11
И так по столбикам , снизу вверх , заполняем все клетки.
n
. 1 2 L L' . . . . . .
. 1 2 . . . . . . . . .
. 1 2 . . . . . . . . .
. 1 2 . . . . . . . .
. 1 2 . . . . . . . .
. 1 2 . . . . . . . .
. 1 2 . . . . . . . .
. 1 2 . . . . . . . . .
9 1 2 . . . . . . . . .
8 1 2 . . . . Lа Lх . .
7 1 2 . . . . Lв . . .
6 1 2 . . . . . . . .
5 1 2 . . . . . . . .
4 1 2 L L'' . . . . . .
3 1 2 L L'' . . . . . .
2 1 2 L L' . . . . . .
1 1 2 3 4 5 6 7 8 9 10 . .
1 2 3 4 5 6 7 8 9 10 . . . g
"Multi multa sciunt , nemo - omnia" |
|
|
| номер сообщения: 49-2-1747 |
|
|
|
|
iourique:
Идентичность формул следует из равенства

Его несложно доказать по индукции, но комбинаторный смысл от меня ускользает... |
Наличие подобных соотношений меня всегда выводила из себя. У меня совершенно нет на них нюха. Неужели есть люди, которые могут придумывать подобное пачками?
В задаче о шариках мне удалось ответить на некоторые вопросы, которые меня давно мучают. Например, пространство однородных полиномов натянутое P_k(z_1,z_2,...,z_N) на (k пробегает значения от нуля до бесконечности) имеет размерность N. Причем в качестве базисных векторов в этом пространстве можно взять собственные функции оператора B. На днях мне удалось явно построить эти базисные вектора, а также я научился находить коэффициенты при z_i^N у этих базисных векторов. В этом подходе решение задачи выглядит так.
1) Выбираем начальное распределение шариков в мешке
2) Находим базисные вектора в виде собственных функций оператора B
3) Раскладываем начальное состояние по базисным векторам
4) Эволюция (перекрашивание шариков) в терминах базисных векторов тривиальна и сводится к умножению на число
5) В каждый момент я умею вычислять вероятность обнаружить в мешке все шарики одного цвета (коэффициенты при z_i^N)
6) Всё.
Вот только особенной красоты я в этом подходе не заметил. Какое-то нагромождение факториалов. Возможно их можно переписать красивее, но я этого не умею.
PS В файл эти изыскания я не добавлял. |
|
|
| номер сообщения: 49-2-1754 |
|
|
|
|
Общая задача:
Есть небоскрёб в L этажей. Имеем n абсолютно одинаковых стеклянных шарика. За какое наименьшее g число бросаний можно гарантированно определить, при бросании с какого наинизшего этажа шарик разбивается.
.....
Таблица
количество шариков
n.....1.....2.....5....11....23....47....95...191...383...767..1535..3071..6143..12287
n-1...1.....2.....5....11....23....47....95...191...383...767..1535..3071..6143..12287
......1.....2.....5....11....23....47....95.....*.....*.....*.....*.....*.....*......*
ni....1.....2.....5....11....23....47....95...191.....*.....*.....*.....*.....*......*
10....1.....2.....5....11....23....47....95.....*.....*.....*.....*..3069..6118..12116
9.....1.....2.....5....11....23....47....95...191...383...767..1533..3048..5997..11610
8.....1.....2.....5....11....23....47....95...191...383...765..1514..2948..5612..10400
7.....1.....2.....5....11....23....47....95...191...381...748..1433..2663..4787...8321
6.....1.....2.....5....11....23....47....95...189...366...684..1229..2123..3533...5681
5.....1.....2.....5....11....23....47....93...176...317...544...893..1409..2147...3173
4.....1.....2.....5....11....23....45....82...140...226...348...515...737..1025...1391
3.....1.....2.....5....11....21....36....57....85...121...166...221...287...365....456
2.....1.....2.....5.....9....14....20....27....35....44....54....65....77....90....104
1.....1.....2.....3.....4.....5.....6.....7.....8.....9....10....11....12....13.....14
......1.....2.....3.....4.....5.....6.....7.....8.....9....10....11....12....13.....14. g бросков
Как получается любое табличное L за 3 , 4 , 5 , 6 и т.д. бросков?
Простой граф!
При помощи довольно несложного графа можем решит и задачу ... " окрашивание шариков".
Надоело... |
|
|
| номер сообщения: 49-2-1756 |
|
|
|
|
LatchezarS:
п.п. Логическая задача особой трудности!
Рассматриваемая задача отличается тем , что в ней число множесв , между злементами которь/х
необходимо установить взаимно-однозначное соответствие , равно не двум, не трем и даже не четь/рем,
а шести (национальность; напиток; что курит; цвет палатки; номер палатки; игра). |
Эх, что-то никто не хочет решать. Я такие задачи в школе решал, у меня даже тетрадка с записями сохранилась. Забавно перелистывать школьные тетради и дневники. Какие там записи!
| Снова не заполнил дневник погоды - 1 |
Жизнь! Я спокойно относился к плохим оценкам, но помню случилась неудачная неделя и у меня на развороте оказалось то ли пять, то ли шесть двоек. Пришлось впервые выдирать листы из дневника. Жаль, что этот шедевр не сохранился. |
|
|
| номер сообщения: 49-2-1757 |
|
|
|
|
MikhailK: LatchezarS:
п.п. Логическая задача особой трудности! |
Эх, что-то никто не хочет решать. |
У меня получилось, что в шахматы играет француз, а любитель водки живёт в палатке #1. |
|
|
| номер сообщения: 49-2-1758 |
|
|
|
|
Roger: MikhailK: LatchezarS:
п.п. Логическая задача особой трудности! |
Эх, что-то никто не хочет решать. |
У меня получилось, что в шахматы играет француз, а любитель водки живёт в палатке #1. |
Одно верно,другое - нет.Т.с. 50%. 
Роджер,
посмотрите пость/ 465 и 467 (нажмите на "цитировать") и таблиць/ если воцможно загрузите
т.с. правильно на форуме.
Я с компом на "Вь/"... Смотрю все задачи и предлагаемь/е рещения,а вот свое мнение "отобразить" математически ,в том числе и графически,никак не могу.
Поможете? |
|
|
| номер сообщения: 49-2-1759 |
|
|
|
|
LatchezarS: посмотрите пость/ 465 и 467 (нажмите на "цитировать") и таблиць/ если воцможно загрузите
т.с. правильно на форуме.
Я с компом на "Вь/"... Смотрю все задачи и предлагаемь/е рещения,а вот свое мнение "отобразить" математически ,в том числе и графически,никак не могу.
Поможете? |
Я тоже не знаю как вставить простую текстовую таблицу. Но можно сделать её картинкой.
Вот примерный ход действий под Windows:
1) форматируете таблицу любым доступным способом (в текстовом виде, Word-е или Excel-е),
2) нажимаете <PrtSc> (спасаете графическую копию экрана в буфер),
3) заходите в граф. редактор, например Paint,
4) нажимаете Ctrl-V (вынимаете картинку из буфера),
5) нажимаете кнопку "Select", выбираете участок экрана с таблицей,
6) из меню Paint выбираете "Edit", "Copy to". Выбираете имя файла, в который спасётся участок картинки с таблицей,
7) из меню Paint выбираете "File", "Open", загружаете файл, спасённый на предыдущем этапе,
8) из меню Paint выбираете "File", "Save as", меняете тип файла на JPEG,
9) вставляете картинку в сообщение.
 |
|
|
| номер сообщения: 49-2-1760 |
|
|
|
|
Roger: MikhailK: LatchezarS:
п.п. Логическая задача особой трудности! |
Эх, что-то никто не хочет решать. |
У меня получилось, что в шахматы играет француз, а любитель водки живёт в палатке #1. |
И у меня так получилось. |
|
|
| номер сообщения: 49-2-1761 |
|
|
|
|
| MikhailK:PS В файл эти изыскания я не добавлял. |
Может, добавишь? |
|
|
| номер сообщения: 49-2-1762 |
|
|
|
|
Хотите решение?! 
По поверхности вроде бь/ так, но неверно.На 50% правильно...но только на 50!
За таблицу - спасибо!
А что скажете о решение задачи о небоскреба ... Кстати зта задача больше логической чем
"вь/числителная , а изпользование простого графа сразу и лекго дает как решение для любого
n g -( Таблица) так и возможностю решат уиму других прямь/х и обратнь/х задач .
А что бь/ присуствовали формуль/ - вот зта важна:
Max число зтажей которь/е можем обслеовать за g бросков.
степень.......(g-2)
Lmax(g)= 3.2 - 1 ( для любого количество n(n> g-1 как и для n = g)
Она позволяет очень бь/стро раздвигать таблицу , чтобь/ обнаружи то что конкретно нам нужно.
п.п. Покажите ее на форуме "правшльно",прошу. |
|
|
| номер сообщения: 49-2-1763 |
|
|
|
|
LatchezarS: Хотите решение?! 
По поверхности вроде бь/ так, но неверно.На 50% правильно...но только на 50!
За таблицу - спасибо!
А что скажете о решение задачи о небоскреба ... |
По поводу задачи про небоскрёб: у Вас маленькая систематическая ошибочка вкралась. Посмотрите, у Вас при 2-х шариках и 2-х бросках ответ - 2 этажа. Однако, правильный ответ - 3 этажа. Первый шарик бросаем со 2-ого этажа, а второй, в зависимости от результата первого броска - с 1-ого или 3-его. Здесь я предполагаю, что этажи считаются с 1-ого. Может быть Вы считаете с 0-ого этажа? Но тогда неправильна уже 1-ая клетка в таблице - для одного шарика и одного броска.
Вот мой частный ответ для 100-этажного дома.
Формулу Вашу я не понял. Если Вы имели в виду

, то это, вроде, не соответствует Вашей таблице. |
|
|
| номер сообщения: 49-2-1764 |
|
|
|
|
Roger: LatchezarS: Хотите решение?! 
По поверхности вроде бь/ так, но неверно.На 50% правильно...но только на 50!
За таблицу - спасибо!
А что скажете о решение задачи о небоскреба ... |
По поводу задачи про небоскрёб: у Вас маленькая систематическая ошибочка вкралась. Посмотрите, у Вас при 2-х шариках и 2-х бросках ответ - 2 этажа. Однако, правильный ответ - 3 этажа. Первый шарик бросаем со 2-ого этажа, а второй, в зависимости от результата первого броска - с 1-ого или 3-его. Здесь я предполагаю, что этажи считаются с 1-ого. Может быть Вы считаете с 0-ого этажа? Но тогда неправильна уже 1-ая клетка в таблице - для одного шарика и одного броска.
Вот мой частный ответ для 100-этажного дома.
Формулу Вашу я не понял. Если Вы имели в виду

, то это, вроде, не соответствует Вашей таблице. |
Почему?
Вас смущает столбик единиц - но он так сказат как "2" среди прость/х чисел. Формула верна за все
g >1.Я пропустил отметит зто.
Граф следующий:
b1->b2
+
a1
(Для улеснения ползую обозначения полей шахматнои доски)
Вертикаль а - зто столбик двоек.
Первая горизонталь - зто ряд при n = 1 : 1 , 2 ,3 ,... g |
|
|
| номер сообщения: 49-2-1765 |
|
|
|
|
Roger: Grigoriy: Ну и ещё одна (знакомая тут многим :-) ) задача на ясное мышление.
Есть небоскрёб в 100 этажей. Имеем 2 абсолютно одинаковых стеклянных шарика. За какое наименьшее число бросаний можно гарантированно определить, при бросании с какого наинизшего этажа шарик разбивается. |
Для математиков ответ, наверное, 14 бросков (вплоть до 105 этажей). |
105 зтажа не успеете - Из условии можно сделать логическое умозаключение , что раз шарик не разбился после броска с 104 зтажа то наинизщего зтажа ..105.Но в условие нигде не указано ,что
после броска с какого то зтажа шарик гарантированно разбивается. |
|
|
| номер сообщения: 49-2-1766 |
|
|
|
|
iourique: | MikhailK:PS В файл эти изыскания я не добавлял. |
Может, добавишь? |
Добавил. Ерунда какая-то получается. Ничего проще первоначального решения не выходит. |
|
|
| номер сообщения: 49-2-1767 |
|
|
|
|
MikhailK: iourique: | MikhailK:PS В файл эти изыскания я не добавлял. |
Может, добавишь? |
Добавил. Ерунда какая-то получается. Ничего проще первоначального решения не выходит. |
Спасибо. |
|
|
| номер сообщения: 49-2-1768 |
|
|
|
|
LatchezarS:
Почему?
Вас смущает столбик единиц - но он так сказат как "2" среди прость/х чисел. Формула верна за все
g >1.Я пропустил отметит зто.
|
Меня смущает, что 3.2 в 12 степени - это порядка миллиона, а в таблице у Вас стоит 12 тысяч.
| LatchezarS: 105 зтажа не успеете - Из условии можно сделать логическое умозаключение , что раз шарик не разбился после броска с 104 зтажа то наинизщего зтажа ..105.Но в условие нигде не указано ,что после броска с какого то зтажа шарик гарантированно разбивается. |
Нет. Если шарики очень прочные, то последний, 14-й бросок, будет со 105 этажа. |
|
|
| номер сообщения: 49-2-1769 |
|
|
|
|
Roger:
Меня смущает, что 3.2 в 12 степени - это порядка миллиона, а в таблице у Вас стоит 12 тысяч.
| LatchezarS: 105 зтажа не успеете - Из условии можно сделать логическое умозаключение , что раз шарик не разбился после броска с 104 зтажа то наинизщего зтажа ..105.Но в условие нигде не указано ,что после броска с какого то зтажа шарик гарантированно разбивается. |
Нет. Если шарики очень прочные, то последний, 14-й бросок, будет со 105 этажа. |
Формула верна.
2 в 12 степени = 4096 , какой милион .
4096.3=12288
1288-1=12287
смотрим в таблицу - за 14 бросков махчисло зтажей которь/е гарантировано можем обследовать
12287
А разве воздвигаете в степени (3.2)!? 
На счет броска со 105 етажа.
Шарик разбился! И что тогда...104 или 105 ? |
|
|
| номер сообщения: 49-2-1770 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2025 гг. |
|
|
|