|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Grigoriy: Да, конечно. Например, Юрик и Роджер наверняка поймут. Поясню. Открыто - значит, если мы достаочно мало изменим оператор - то он останется отображением "на" |
Признаюсь, что техникой решения таких задач я не владею, надо лезть в учебник.
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-1680 |
|
|
|
|
Grigoriy: Самолёт-разведчик летает по кругу радиусом 200 км со скоростью 1000 км/час. Из центра круга вылетает ракета с той же скоростью, всё время направленная на самолёт. Как скоро она поразит самолёт?
Задача забавна "ответом". Но я его увидел только после того, как решил её аналитически(это тривиально). Интересно было бы геометрическое решение :-) |
Я неточно воспринял условие и его соответственно набил тут :-) :-(
В книжке сказано так: "ракета управляется так, что всё время находится на прямой центр-самолёт". Для меня это было так, что её скорость направлена на самолёт :-(
Прошу прощения :-( |
|
|
| номер сообщения: 49-2-1681 |
|
|
|
|
Если "на прямой" то вроде проще решается. Хотя нет, со скоростью ещё проще. 
__________________________
Audiatur et altera pars |
|
|
| номер сообщения: 49-2-1682 |
|
|
|
|
iourique: | MikhailK: Эх, а я всё ещё ломаю голову решая задачу iourique о шариках в мешке. После длительной паузы снова на неё набросился и даже имеется некоторое продвижение. В этой задаче у меня начали появляться разные алгебраические структуры, что позволило мне серьезно напрячь знакомых алгебраистов. Посмотрим что они скажут. |
Любопытно - расскажите, что получится/получается. Может, статью напишем  . |
Обошелся без алгебраистов  . Ответ получился (N-1)*(N-1), где N - число шаров в мешке. Решение у меня получилось не очень короткое, но идеологически простое.
Интересно, что скажут алгебраисты. Завтра узнаю.
Добавлено.
Как обычно бывает, математики помочь не смогли. Хотя польза от них несомненно есть. После обсуждения с ними задачи у меня появилось несколько идей, которые и позволили добить задачу. |
|
|
| номер сообщения: 49-2-1683 |
|
|
|
|
Grigoriy: Grigoriy: Самолёт-разведчик летает по кругу радиусом 200 км со скоростью 1000 км/час. Из центра круга вылетает ракета с той же скоростью, всё время направленная на самолёт. Как скоро она поразит самолёт?
Задача забавна "ответом". Но я его увидел только после того, как решил её аналитически(это тривиально). Интересно было бы геометрическое решение :-) |
Я неточно воспринял условие и его соответственно набил тут :-) :-(
В книжке сказано так: "ракета управляется так, что всё время находится на прямой центр-самолёт". Для меня это было так, что её скорость направлена на самолёт :-(
Прошу прощения :-( |
С ТАКОЙ РАКЕТОЙ...И ОПЕРАТОРОМ
Чтобь/ вообшюще поразит самолета (V ракеть/= Vсамолета = 1000 км/ч ;R окружности = 200 km)оператор должен запустит ракету с углом опережения 5,324 градуса и держат курс ракеть/ строго по радиусу .
Как опрделилис зти 57.324 градуса?
Ракета должна переодолет минимум 200 км до самолета,следовательно время подлета 12 мин . (200 : 1000)х 60 = 12 мин
За зто время (12 мин) самолет передвинется по дуге на 57.324 градусов ((200х2)х3,14):200 = 6.28
360:6.28 = 57.324 градусов
Так что , задача имеет однозначний ответ - оператор дурак и он самолет не поразит никогда. |
|
|
| номер сообщения: 49-2-1688 |
|
|
|
|
| Лачезар, из условий задачи не следует, что самолёт всё время летит в одну и ту же сторону. |
|
|
| номер сообщения: 49-2-1689 |
|
|
|
|
| номер сообщения: 49-2-1690 |
|
|
|
|
| Roger: Лачезар, из условий задачи не следует, что самолёт всё время летит в одну и ту же сторону. |
Роджер,разве самолет...НЛО? ...Такие задачки  .
Дед говорил " Люди не одинаковь/е ,умнь/е,дураки и одна особая группа - на-ученнь/е.Так что читай ,но и хорошо думай сам!" |
|
|
| номер сообщения: 49-2-1699 |
|
|
|
|
Grigoriy:  |
Интересно, кто это такой? Похоже на кошачью морду без ушей. |
|
|
| номер сообщения: 49-2-1700 |
|
|
|
|
| Пиррон, это всё-таки превьюшка. Посмотрите картинку. |
|
|
| номер сообщения: 49-2-1701 |
|
|
|
|
| LatchezarS: Роджер,разве самолет...НЛО? |
Хуже того - он разведчик. Ну и вообще ракет боится очень. |
|
|
| номер сообщения: 49-2-1702 |
|
|
|
|
Grigoriy: Grigoriy: Самолёт-разведчик летает по кругу радиусом 200 км со скоростью 1000 км/час. Из центра круга вылетает ракета с той же скоростью, всё время направленная на самолёт. Как скоро она поразит самолёт?
Задача забавна "ответом". Но я его увидел только после того, как решил её аналитически(это тривиально). Интересно было бы геометрическое решение :-) |
Я неточно воспринял условие и его соответственно набил тут :-) :-(
В книжке сказано так: "ракета управляется так, что всё время находится на прямой центр-самолёт". Для меня это было так, что её скорость направлена на самолёт :-(
Прошу прощения :-( |
Чтобь/ все бь/ло ясно:
Задача:
" Оператор А двигает (туда-сюда) солнечнь/й зайчик строго по кругу с радиусом 200 мет, с постоянной скоростю 1000 мет/мин.
Оператор В начинает двигат свой солнечнь/й зайчик из центра круга с такой же постоянной скоростью - 1000 мет/мин.Оператор В должен вести свой зайчик так, что центр и солнечнь/е зайчики всегда
находились на одной прямой линии.
Оператор В побеждает если зайчик-В накроет зайчик-А,если нет - проигрь/вает.
п.п.
Наблюдение, контроль и констатация факта накрития зайчиков ,осуществляет астроном С - с 25-сантиметровым рефлектором используя увеличения 76х215; и 214х215; и спектрометром для измерения блеска зайчиков.
Кто победит??"
Так или не так? Что еще надо уточнит ? |
|
|
| номер сообщения: 49-2-1703 |
|
|
|
|
iourique: Вброшу еще задачку ...
В мешке лежит несколько шаров, выкрашенных в разные цвета (изначально, все шары - разного цвета). За ход мы наугад вытаскиваем шар из мешка, затем (не возвращая первый шар в мешок), вытаскиваем второй шар и перекрашиваем его в цвет первого. После этого оба шара кладутся обратно в мешок, мешок встряхивается (энергично) и все по новой. Вопрос: в среднем за сколько шагов все шары будут перекрашены в один цвет?
примеры:
1 шар - 0 шагов.
2 шара - 1 шаг.
3 шара - 4 шага (после первого имеем два одноцветных шара и третий другого цвета. вероятность перекрасить третий за один шаг - 1/3, соответственно в среднем нужно еще 3 шага).
Ответ в общем случае уже можно угадать . Доказать тоже можно, но ничего убедительного я не нашел. |
IOURIGUE , заключение- "3 шара - 4 шага (после первого имеем два одноцветных шара и третий другого цвета. вероятность перекрасить третий за один шаг - 1/3, СООТВЕТСТВЕННО В СРЕДНЕМ НУЖНО ЕЩЕ 3 ШАГА)." - абсолютно неверно.
Почему?
Пусть 3 шара окрашеннь/ в цветов россиского флага.
После первого шага/перкрашивания имеем в мешке со 100% вероятностю окрашеност 1 1 2.
(1 - белое,синьее или красное ; 2 - раличное от 1)
В процесе второго перекрашивания возможно:
а) - с вероятность 2/3 вь/таскиваем шар окраской 1.
дальше
с вероятность 1/2 вь/таскиваем шар с окраской 2 - задача решена - вероятность зтого равна
2/3 х 1/2 = 1/3
с вероятность 1/2 вь/таскиваем шар тоже с окраской 1,"перекрашиваем" опять в 1-ДЛЯ ВЬ/ПОЛНЕНИЯ УСЛОВИИ ЗАДАЧИ ! Следовательно с вероятностью 2/3 х 1/2 = 1/3 НЕ ОКРАСИМ ШАРИКИ ОДИНАКОВО :
Wa(неокрашивания шаров одинаково в случаем а) = 1/3
б) - с вероятность 1/3 можем вь/ташит шар с цветом 2.Тогда после всех остальньих действии окраска
шариков будет неодинакова - 1 2 2.И В ЗТОМ СЛУЧАЕ НЕ ОКРАСИМ ШАРИКИ ОДИНАКОВО с вероятностью
1/3 х 1 = 1/3. Следовательно
Wб(неокрашивания шаров одинаково в случаем б)= 1/3.
Сумма вероятностей Wa + Wб = 1/3 + 1/3 = 2/3 = W2 верояъность неокрашивания шаров одинаково
после 2 шага.
Что дальше?
Все повторяется точь в точь - конечьно имеем ввиду только зти 66.66% случаев где после второго шага/окрашивания ситуация не изменилас - в мешке опять шарики 1 1 2(или 1 2 2 - фактически одно и тоже ).
Тогда W3 (вероятность неокрашивания шариков одинаково после 3 шага)= W2 х 2/3 = 4/9
W4 (вероятность неокрашивания шариков одинаково после 4 шага)= W3 х 2/3 = 8/27СЛЕДОВАТЕЛЬНО ЗА 4 ШАГА/ПЕРЕКРАШЬ/ВАНИЯ МОЖЕМ БЬ/ТЬ УВЕРЕНЬ/,ЧТО ВСЕ 3 ШАРИКА ОКРАШЕНЬ/ ОДИНАКОВО
ТОЛЬКО НА 70.37% Точнее 100(1 - 8/27)%.
Общая формула (мь/ сейчас ее вь/вели ,смотрите вверх)
(n -1)
2
Wn = ---------- вероятность неокрашивания 3 шариков одинаково после n шагов
(n -1)
3
Так что для вь/полнения задания о одинаковой окраски 3 шариков с вероятностю p > 99 % , ( процент и не так уж большой если заложили свою жизнь! ), нужнь/ минимум 12 шагов!
p = 100 х( 1 - Wn) если n=12,то p = 100 ( 1 - 4096 : 531447)= 99.22 % что > 99 %.
А общая задача о N шариков в мешке...и т.д. зто сл-о-о-ожная вещь! Ответит можно , но как говорил Чапаев "- Пахнет литром,но доказать не могу!"
Давайте лучьше посмотреть на "Амбер 2009". |
|
|
| номер сообщения: 49-2-1704 |
|
|
|
|
| LatchezarS: IOURIGUE , заключение- "3 шара - 4 шага (после первого имеем два одноцветных шара и третий другого цвета. вероятность перекрасить третий за один шаг - 1/3, СООТВЕТСТВЕННО В СРЕДНЕМ НУЖНО ЕЩЕ 3 ШАГА)." - абсолютно неверно. |
| Так что для вь/полнения задания о одинаковой окраски 3 шариков с вероятностю p > 99 % ... |
Разные вещи. |
|
|
| номер сообщения: 49-2-1705 |
|
|
|
|
MikhailK: iourique: | MikhailK: Эх, а я всё ещё ломаю голову решая задачу iourique о шариках в мешке. После длительной паузы снова на неё набросился и даже имеется некоторое продвижение. В этой задаче у меня начали появляться разные алгебраические структуры, что позволило мне серьезно напрячь знакомых алгебраистов. Посмотрим что они скажут. |
Любопытно - расскажите, что получится/получается. Может, статью напишем . |
Обошелся без алгебраистов . Ответ получился (N-1)*(N-1), где N - число шаров в мешке. Решение у меня получилось не очень короткое, но идеологически простое.
Интересно, что скажут алгебраисты. Завтра узнаю.
Добавлено.
Как обычно бывает, математики помочь не смогли. Хотя польза от них несомненно есть. После обсуждения с ними задачи у меня появилось несколько идей, которые и позволили добить задачу. |
MikhailK, мое решение было не вполне удовлетворительным - я угадал формулу для произвольного распределения цветов, а потом доказал ее. Не пришлете свое решение (если не хотите здесь, можно по емайлу: volvovskiy at yahoo dot com)? |
|
|
| номер сообщения: 49-2-1706 |
|
|
|
|
iourique:
MikhailK, мое решение было не вполне удовлетворительным - я угадал формулу для произвольного распределения цветов, а потом доказал ее. Не пришлете свое решение (если не хотите здесь, можно по емайлу: volvovskiy at yahoo dot com)? |
ОК, в выходные приготовлю решение. Вчера у меня появились в этой задаче любопытные соотношения, но, к сожалению, ничего нового они не принесли. |
|
|
| номер сообщения: 49-2-1707 |
|
|
|
|
| MikhailK: ОК, в выходные приготовлю решение. Вчера у меня появились в этой задаче любопытные соотношения, но, к сожалению, ничего нового они не принесли. |
Спасибо. |
|
|
| номер сообщения: 49-2-1708 |
|
|
|
|
iourique: | MikhailK: ОК, в выходные приготовлю решение. Вчера у меня появились в этой задаче любопытные соотношения, но, к сожалению, ничего нового они не принесли. |
Спасибо. |
iourique: Вброшу еще задачку ...
В мешке лежит несколько шаров, выкрашенных в разные цвета (изначально, все шары - разного цвета). За ход мы наугад вытаскиваем шар из мешка, затем (не возвращая первый шар в мешок), вытаскиваем второй шар и перекрашиваем его в цвет первого. После этого оба шара кладутся обратно в мешок, мешок встряхивается (энергично) и все по новой. Вопрос: в среднем за сколько шагов все шары будут перекрашены в один цвет?
примеры:
1 шар - 0 шагов.
2 шара - 1 шаг.
3 шара - 4 шага (после первого имеем два одноцветных шара и третий другого цвета. вероятность перекрасить третий за один шаг - 1/3, соответственно в среднем нужно еще 3 шага).
Ответ в общем случае уже можно угадать . Доказать тоже можно, но ничего убедительного я не нашел. |
Готово. Что-то длинное решение у меня получилось. Пять страниц выкладок.
Решение в формате HTML
Решение в формате PDF |
|
|
| номер сообщения: 49-2-1710 |
|
|
|
|
MikhailK:
Решение в формате HTML
Решение в формате PDF |
Осталось узнать, где этот file:///home/
PS А всё-равно не работает - сервер не отвечает |
|
|
| номер сообщения: 49-2-1711 |
|
|
|
|
Roger: MikhailK:
Решение в формате HTML
Решение в формате PDF |
Осталось узнать, где этот file:///home/ |
Шустрый какой. Я эту ошибку исправил в течении 30 секунд.
Все работает! |
|
|
| номер сообщения: 49-2-1712 |
|
|
|
|
Да, это я случайно смотрел с IP адреса одного университета. От него весь Ваш домен не виден - то ли с конкурентами борются, то ли с ересью. |
|
|
| номер сообщения: 49-2-1713 |
|
|
|
|
Roger:
Да, это я случайно смотрел с IP адреса одного университета. От него весь Ваш домен не виден - то ли с конкурентами борются, то ли с ересью. |
с ересью, с ересью  |
|
|
| номер сообщения: 49-2-1714 |
|
|
|
|
Посмотрел я сейчас свежим взглядом свой вчерашний текст и сразу нашел несколько досадных мелких опечаток. По ссылкам теперь исправленная версия. |
|
|
| номер сообщения: 49-2-1715 |
|
|
|
|
MikhailK:
Посмотрел я сейчас свежим взглядом свой вчерашний текст и сразу нашел несколько досадных мелких опечаток. По ссылкам теперь исправленная версия. |
Спасибо. Сурово - долго прорубался. Решение более логично (и соответственно лучше), чем мое - ничего не надо угадывать, хотя основной недостаток (?) тот же: ответ существенно проще, чем выкладки, остается ощущение необъясненности происходящего. Надо еще подумать. |
|
|
| номер сообщения: 49-2-1716 |
|
|
|
|
iourique: MikhailK:
Посмотрел я сейчас свежим взглядом свой вчерашний текст и сразу нашел несколько досадных мелких опечаток. По ссылкам теперь исправленная версия. |
Спасибо. Сурово - долго прорубался. Решение более логично (и соответственно лучше), чем мое - ничего не надо угадывать, хотя основной недостаток (?) тот же: ответ существенно проще, чем выкладки, остается ощущение необъясненности происходящего. Надо еще подумать. |
Я прикинул и у меня получилось, что высшие моменты числа перекрашиваний уже не будут описываться столь простой формулой. В случае второго момента возникают суммы от 1/(k*k), где k пробегает от 1 до N.
Интересно, а как ведет себя величина (1-p_k) при больших k? У меня есть формула для p_k в виде конечного куска знакопеременного ряда, но по ней затруднительно сделать эту оценку. |
|
|
| номер сообщения: 49-2-1717 |
|
|
|
|
| Я бы назвал процесс перекраски шариков "дискретным броуновским движением" |
|
|
| номер сообщения: 49-2-1718 |
|
|
|
|
| MikhailK: Интересно, а как ведет себя величина (1-p_k) при больших k? У меня есть формула для p_k в виде конечного куска знакопеременного ряда, но по ней затруднительно сделать эту оценку. |
Если я нигде не проврался, то из Ваших формул следует, что (1-p_k) асимптотически стремится к 3(N-2)/N * (1 - 2/(N(N-1)))^(k-1). |
|
|
| номер сообщения: 49-2-1719 |
|
|
|
|
iourique: | MikhailK: Интересно, а как ведет себя величина (1-p_k) при больших k? У меня есть формула для p_k в виде конечного куска знакопеременного ряда, но по ней затруднительно сделать эту оценку. |
Если я нигде не проврался, то из Ваших формул следует, что (1-p_k) асимптотически стремится к 3(N-2)/N * (1 - 2/(N(N-1)))^(k-1). |
А у меня получается
3(N-1)/(N+1)*(1 - 2/(N(N-1)))^(k-1)
Свой вывод я поместил в дополнение 4. |
|
|
| номер сообщения: 49-2-1720 |
|
|
|
|
Мое решение выглядит так: пусть A(n_1, n_2,..,n_N)- число шагов, требуемое для перекраски n_1 шариков цвета 1, n_2 шариков цвета 2, и т.д. в один цвет. Тогда
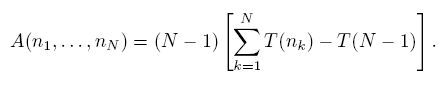
Здесь используется обозначение
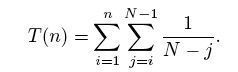
Формула угадана наблюдением за случаем 6 шариков . Доказательство очень просто - проверить, что А удовлетворяет системе линейных уравнений. В частности, А(1,1,...,1)=(N-1)*(N-1). |
|
|
| номер сообщения: 49-2-1721 |
|
|
|
|
iourique:
Здесь используется обозначение
|
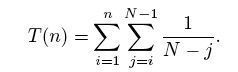
А почему индекс i не встречается под знаком суммы?
Интересно, а как твое общее решение можно получить в рамках моего подхода? |
|
|
| номер сообщения: 49-2-1722 |
|
|
| |
|
|
|
|
|
|
|
| Copyright chesspro.ru 2004-2024 гг. |
|
|
|
